Основні властивості інтеграла Лебега від довільної функції.
Скрізь нижче в цьому параграфі  є
є  -вимірна підмножина множини
-вимірна підмножина множини  , на якій визначені функції
, на якій визначені функції 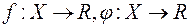 .
.
Безпосередньо із означення інтеграла Лебега від довільної функції випливають наступні його властивості:
1) 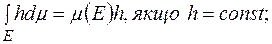
2) 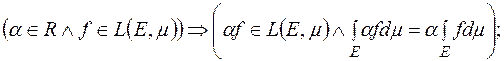
3) 
В справедливості властивостей 2),3) переконуємося на основі граничного переходу та відповідних властивостей інтеграла Лебега від простих функцій.
Спреведливі також властивості:
4) 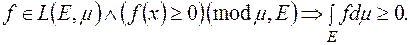
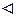 Існує послідовність простих
Існує послідовність простих  -інтегровних на
-інтегровних на  невідємних функцій
невідємних функцій 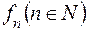 така, що
така, що 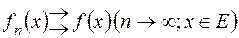 ,
, 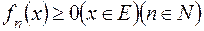 . Тоді
. Тоді 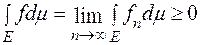 , оскільки
, оскільки 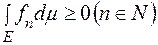 .
. 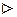
5) 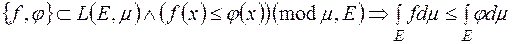
 Властивість доводиться на основі попередньої властивості.
Властивість доводиться на основі попередньої властивості. 
6) 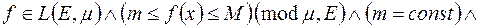
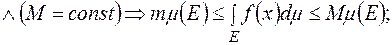
 Це твердження випливає із властивостей 1),5).
Це твердження випливає із властивостей 1),5). 
7)  , зокрема
, зокрема
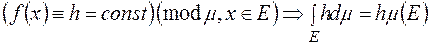 ,
,
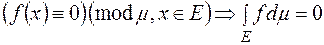 .
.
8) Довільна функція 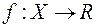 є
є  -інтегровна на
-інтегровна на  -вимірній множині
-вимірній множині 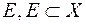 , такій що
, такій що  , і при цьому
, і при цьому 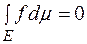 .
.
9) 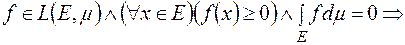
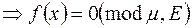 .
.
10) 
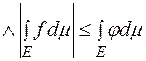 .
.
11) 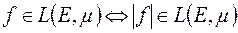 .
.
12) 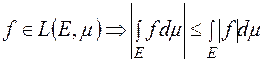 .
.
 Якщо
Якщо  , то, згідно із попередньою властивістю
, то, згідно із попередньою властивістю 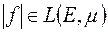 . Якщо
. Якщо 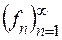 послідовність простих
послідовність простих 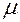 -вимірних і
-вимірних і  -інтегровних на
-інтегровних на  функцій таких, що
функцій таких, що 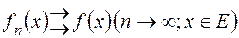 , то
, то 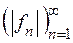 послідовність простих
послідовність простих  -вимірних і
-вимірних і  -інтегровних на
-інтегровних на  функцій таких, що
функцій таких, що 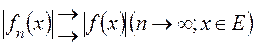 .
.
Оскільки 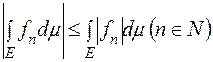 , то переходячи в цій нерівності до границі при
, то переходячи в цій нерівності до границі при 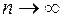 дістанемо
дістанемо  .
. 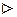
Зазначимо, що сформульовані вище властивості справедливі і у випадку, коли 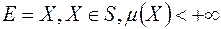 .
.
Дата добавления: 2015-07-24; просмотров: 655;
