Сігма-аддитивність та абсолютна неперервність інтеграла Лебега.
Нехай 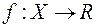 є
є  -інтегровна функція на множині
-інтегровна функція на множині 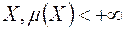 . Тоді, як відомо, функція
. Тоді, як відомо, функція 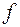
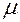 -інтегровна і на кожній
-інтегровна і на кожній  -вимірній підмножині
-вимірній підмножині  множини
множини 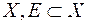 . З'ясуємо тут основні властивості функції
. З'ясуємо тут основні властивості функції
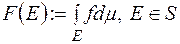 (1)
(1)
що визначена на сігма-алгебрі 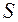 всіх
всіх  -вимірних підмножин множини
-вимірних підмножин множини 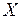 ,
, 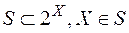 . Справедливі наступні твердження.
. Справедливі наступні твердження.
1. Якщо 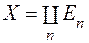 і всі множини
і всі множини 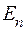 (їх зчисленна або скінченна сукупність) є
(їх зчисленна або скінченна сукупність) є  -вимірні і попарно не перетинаються, а функція
-вимірні і попарно не перетинаються, а функція 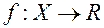 сумовна на
сумовна на 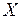 , то вона сумовна на кожній множині
, то вона сумовна на кожній множині 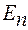 і справедлива рівність
і справедлива рівність
 (2)
(2)
причому ряд із правої частини збігається абсолютно.
Зазначимо, що сформульоване твердження називається властивістю 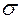 -аддитивності інтеграла Лебега, оскільки рівність (2) можна записати у вигляді
-аддитивності інтеграла Лебега, оскільки рівність (2) можна записати у вигляді
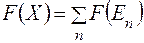 .
.
2. Якщо 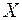 і
і  множини із попереднього твердження,
множини із попереднього твердження, 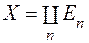 , а функція
, а функція 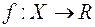 сумовна на кожній множині
сумовна на кожній множині  причому ряд
причому ряд
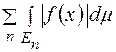
збігається, то функція 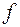 сумовна на множині
сумовна на множині 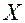 і
і
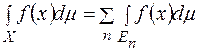 .
.
3. Інтеграл Лебега (1), як функція множин, є абсолютно неперервна функція тобто, якщо функція 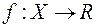 сумовна на множині
сумовна на множині 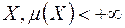 то
то
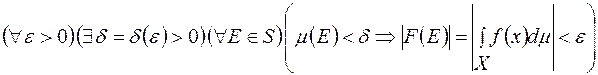
Із сформульованих тверджень випливає, що при невідємній і сумовній на 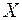 функції
функції 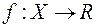 функція
функція 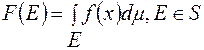 , є також невідємна і
, є також невідємна і 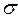 -адитивна на
-адитивна на 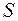 тобто вона являє собою міру таку, що
тобто вона являє собою міру таку, що 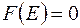 , коли
, коли 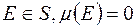 .
.
Дата добавления: 2015-07-24; просмотров: 666;
