Прості функції та їх інтеграл Лебега.
Будемо тут розглядати простір 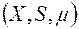 із повною мірою
із повною мірою 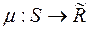 , визначеною на
, визначеною на 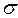 -алгебрі
-алгебрі 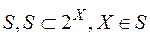 , причому
, причому 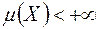 .
.
Функція 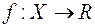 ,
, 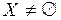 , називається простою. якщо вона приймає на
, називається простою. якщо вона приймає на 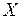 лише скінченну або зчисленну сукупність попарно різних значень
лише скінченну або зчисленну сукупність попарно різних значень
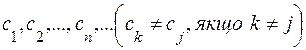 .
.
Очевидно, якщо позначити 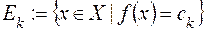 , то
, то 
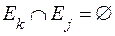 при
при 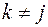 і справедлива рівність
і справедлива рівність
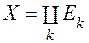 . (1)
. (1)
Тоді проста функція 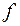 єдиним способом може бути записана у вигляді
єдиним способом може бути записана у вигляді
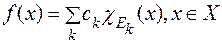 (2)
(2)
де 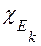 -характеристична функція множини
-характеристична функція множини 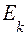 ,
, 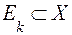 ,тобто така функція, що
,тобто така функція, що 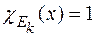 , якщо
, якщо 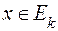 , і
, і 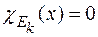 , якщо
, якщо 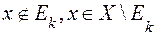 .
.
Можна показати, що проста функція 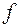 , яка записана у вигляді (2), де
, яка записана у вигляді (2), де 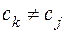 при
при 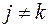 , є
, є  -вимірна (на множині
-вимірна (на множині 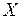 ) тоді і лише тоді, коли всі множини
) тоді і лише тоді, коли всі множини 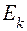 є
є  -вимірні.
-вимірні.
Можна показати, що справедливе також наступне твердження.
Теорема. Функція 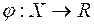 є
є  -вимірна (на множині
-вимірна (на множині 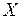 ) тоді і лише тоді, коли існує послідовність
) тоді і лише тоді, коли існує послідовність 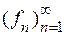 простих
простих  -вимірнмх (на
-вимірнмх (на 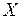 ) функцій
) функцій 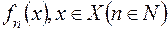 , яка збігається рівномірно на множині
, яка збігається рівномірно на множині 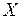 до функції
до функції 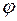
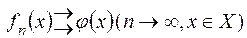 .
.
Нехай 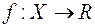 є проста і вимірна (на
є проста і вимірна (на 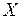 ) функція, що зображена у вигляді (2), де
) функція, що зображена у вигляді (2), де 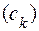 -скінченна або зчисленна послідовність всіх попарно різних її значень на
-скінченна або зчисленна послідовність всіх попарно різних її значень на 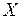 , занумерованих в довільному порядку, і справедлива рівність (1), де всі множини
, занумерованих в довільному порядку, і справедлива рівність (1), де всі множини 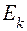 є
є  -вимірні. Нехай
-вимірні. Нехай  -довільна
-довільна  -вимірна підмножина множини
-вимірна підмножина множини 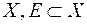 . Тоді у відповідності із рівністю (2) утворимо числовий ряд
. Тоді у відповідності із рівністю (2) утворимо числовий ряд
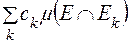 (3)
(3)
Означення. Якщо ряд (3) абсолютно збігається, то проста  -вимірна (на
-вимірна (на 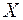 ) функція
) функція 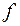 називається інтегровною за Лебегом або сумовною (
називається інтегровною за Лебегом або сумовною (  -інтегровною або
-інтегровною або 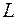 -інтегровною) на множині
-інтегровною) на множині 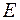 а сума цього ряду називається інтегралом Лебега від функції
а сума цього ряду називається інтегралом Лебега від функції 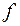 по множ
по множ 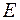 і позначається
і позначається 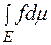 або
або 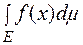 або
або 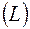
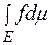 ,
,
тобто
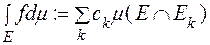 .
.
Зрозуміло, що попереднє означення в силі і тоді, коли 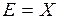 . В цьому випадку інтегровність за Лебегом простої
. В цьому випадку інтегровність за Лебегом простої  -вимірної функції
-вимірної функції 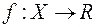 на множині
на множині 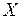 означає абсолютну збіжність ряду
означає абсолютну збіжність ряду
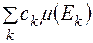 причому
причому  .
.
Якщо проста  -вимірна функція
-вимірна функція 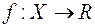 є
є  -інтегровна на
-інтегровна на  -вимірній множині
-вимірній множині 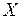 , то вона
, то вона  -інтегровна і на кожній
-інтегровна і на кожній  -вимірній її підмножині
-вимірній її підмножині 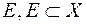 . Такий висновок випливає із попереднього означення та нерівностей
. Такий висновок випливає із попереднього означення та нерівностей
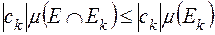 .
.
При умовах, вказаних на початку параграфа, справедливі наступні твердження.
1. Якщо прості  -вимірні функції
-вимірні функції 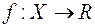 ,
, 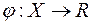
 -інтегровні на
-інтегровні на  -вимірній множині
-вимірній множині  ,
, 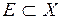 , і
, і 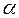 -фіксоване дійсне число,
-фіксоване дійсне число, 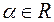 , то функції
, то функції 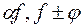 також прості,
також прості,  -вимірні на
-вимірні на 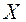 і
і  -інтегровні на
-інтегровні на 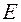 , причому
, причому
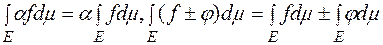 .
.
2. Якщо проста  -вимірна функція
-вимірна функція 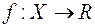 обмежена на
обмежена на  -вимірній множині
-вимірній множині 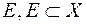 , тобто
, тобто 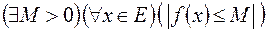 , то вона
, то вона  -інтегровна на
-інтегровна на  , причому
, причому 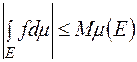 .
.
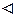 Оскільки
Оскільки 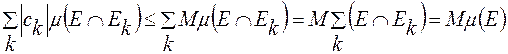
то функція 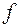
 -інтегровна на
-інтегровна на  . Окрім того
. Окрім того 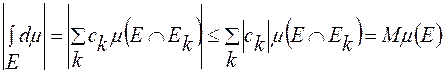 .
. 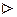
3. Якщо 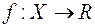 є проста і
є проста і  -вимірна функція, то функція
-вимірна функція, то функція 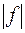 є також проста і
є також проста і  -вимірна на
-вимірна на 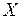 , причому функція
, причому функція 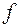 та
та 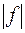 одночасно сумовні або несумовні на кожній
одночасно сумовні або несумовні на кожній  -вимірній множині
-вимірній множині 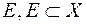 .
.
Зрозуміло, що вказані три твердження справедливі і у впадку, коли 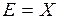 .
.
§.3.2. Інтеграл Лебега від довільної функції.
Будемо вважати, що виконуються всі умови, вказані на початку цього розділу. Нехай  -довільна
-довільна  -вимірна множина,
-вимірна множина, 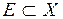 , і
, і 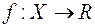 -функція, яка приймає на
-функція, яка приймає на 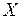 довільні дійсні значення.
довільні дійсні значення.
Означення. Функція 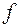 називається сумовною або інтегровною за Лебегом (
називається сумовною або інтегровною за Лебегом (  -інтегровною або
-інтегровною або 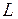 -інтегровною ) на множині
-інтегровною ) на множині  , якщо існує послідовність
, якщо існує послідовність 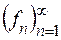 простих
простих  -вимірних і
-вимірних і  -інтегровних на
-інтегровних на  функцій
функцій 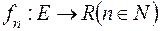 , яка рівномірно збігається на
, яка рівномірно збігається на  до функції
до функції 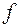 ,
,
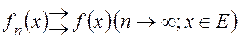 .
.
При цьому границя
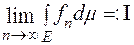 (1)
(1)
називається інтегралом Лебега від функції 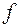 по множині
по множині  і позначається
і позначається 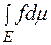 або
або 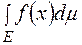 тобто
тобто
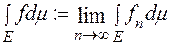 .
.
Зрозуміло, що сформульоване означення в силі і тоді, коли 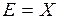 .
.
Можна переконатися в коректності попереднього означення, тобто в справедливості наступних тверджень:
а) границя (1) існує скінченна для кожної послідовності 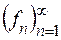 , вказаної в означенні;
, вказаної в означенні;
б) при заданій функції 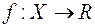 границя (1) не залежить від вибору послідовності
границя (1) не залежить від вибору послідовності 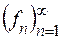 , вказаної в означенні;
, вказаної в означенні;
в) для простої 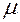 -вимірної на
-вимірної на 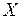 функції
функції 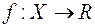 сформульоване тут означення інтеграла рівносильне аналогічному означенню із попереднього параграфа.
сформульоване тут означення інтеграла рівносильне аналогічному означенню із попереднього параграфа.
Справді, згідно із властивостями інтеграла Лебега від простих функцій
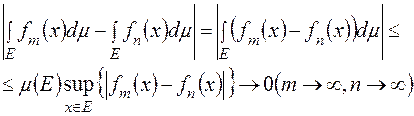
тобто послідовність 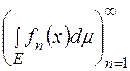 ,як числова послідовність, збігається(за критерієм Коші).
,як числова послідовність, збігається(за критерієм Коші).
Якщо припустити, що існують дві послідовності 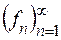 та
та 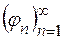 , складені із простих,
, складені із простих,  -вимірних і
-вимірних і  -інтегровних на
-інтегровних на  функцій, таких, що
функцій, таких, що 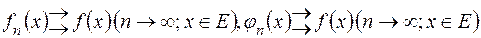 ,
,
але  , причому
, причому 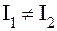 , то розглянемо послідовність
, то розглянемо послідовність
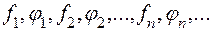 (2)
(2)
Очевидно, послідовність (2) також збігається рівномірно на  до функції
до функції 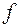 , але послідовність інтегрілів Лебега по
, але послідовність інтегрілів Лебега по  від її членів розбіжна. Одержана суперечність із першим твердженням показує справедливість другого твердження.
від її членів розбіжна. Одержана суперечність із першим твердженням показує справедливість другого твердження.
Для доведення третього твердження, в якому роль функції 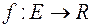 має відігравати проста функція, достатньо розглянути таку послідовність
має відігравати проста функція, достатньо розглянути таку послідовність 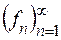 простих функцій
простих функцій 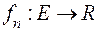 , що
, що 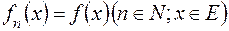 .
.
Зазначимо, що функція 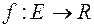 є
є  -інтегровна по кожній
-інтегровна по кожній  -вимірній підмножині
-вимірній підмножині  множини
множини 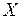 ,
, 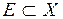 , якщо вона
, якщо вона  -інтегровна по множині
-інтегровна по множині 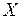 , і при цьому , легко переконатися,що
, і при цьому , легко переконатися,що
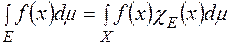 .
.
Оскільки границя послідовності  -вимірних на множині
-вимірних на множині  функцій є
функцій є  -вимірна функція на
-вимірна функція на  , то із попереднього означення випливає, що кожна
, то із попереднього означення випливає, що кожна  -інтегровна на множині
-інтегровна на множині 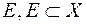 , функція
, функція 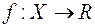 є
є  -вимірна на множині
-вимірна на множині  , тобто
, тобто  -вимірність функції
-вимірність функції 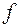 на
на  є необхідна умова її
є необхідна умова її  -інтегровності на множині
-інтегровності на множині  .
.
Згідно із відповідною теоремою попереднього параграфа, для  -вимірної і обмеженої на
-вимірної і обмеженої на  -вимірній множині
-вимірній множині 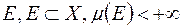 , фукції
, фукції 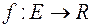 існує послідовність
існує послідовність 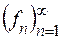
 -вимірних, обмежених на
-вимірних, обмежених на  і простих функцій
і простих функцій 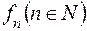 , яка збігається рівномірно на
, яка збігається рівномірно на  до функції
до функції 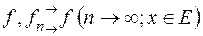 .
.
Оскільки кожна обмежена,  -вимірна проста функція є
-вимірна проста функція є  -інтегровна на
-інтегровна на  , то, згідно із попереднім означенням, обмежена на
, то, згідно із попереднім означенням, обмежена на 
 -вимірна функція
-вимірна функція 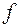 є сумовна на
є сумовна на  .Звичайно, що існують і необмежені функції, що сумовні на даній
.Звичайно, що існують і необмежені функції, що сумовні на даній  -вимірній множині
-вимірній множині  .
.
Зазначимо, що клас всіх  -інтегровних на множині
-інтегровних на множині  функцій позначають
функцій позначають 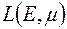 .
.
Дата добавления: 2015-07-24; просмотров: 1094;
