Порівняння лебегового і ріманового інтегралів. Критерій інтегровності за Ріманом.

Зв'язок між інтегралами Лебега і Рімана встановлює наступне твердження.

Теорема. Якщо функція 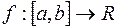інтегровна за Ріманом на 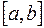, то вона інтегровна також і за Лебегом на 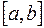тобто

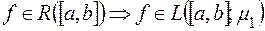причому

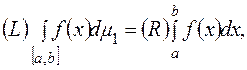
де -міра Лебега на числовій прямій .

Зауваження. Можна навести приклади -вимірних та обмежених на функцій, які інтегровні за Лебегом на 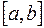і неінтегровні за Ріманом на 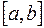. Так відома функція Діріхле 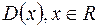, така, що 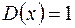, якщо 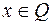і 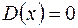, якщо 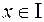, інтегровна за Лебегом на 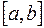, як обмежена і 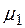-вимірна функція,однак ця функція не інтегровна за Ріманом на 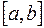, оскільки нижня 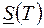та верхня суми Дарбу для неї, які відповідають розбиттю ,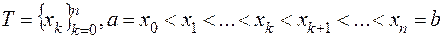

сегмента 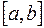, мають вигляд

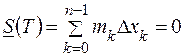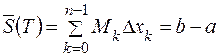, , де

, ,

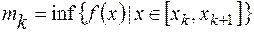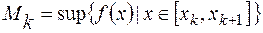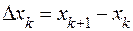, і ,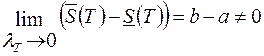

де .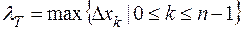

Сформулюємо критерій інтегровності за Ріманом в термінах міри.

Теорема. Для того щоб обмежена на 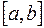функція 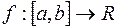була інтегровною за Ріманом на 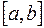необхідно і достатньо, щоб значення лінійної лебегової міри множини 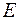всіх її точок розриву дорівнювало нулю, .

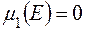Приклад 1. Функція 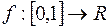така, що 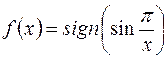при 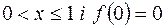, інтегровна за Ріманом на 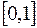, оскільки вона обмежена на 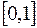і множина 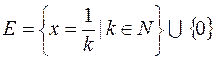всіх її точок розриву 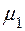-вимірна і .

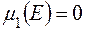Приклад 2. Вказана вище, функція Діріхле 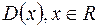,не є інтегровною за Ріманом на 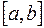, оскільки вона розривна в кожній точці із 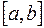, тобто для неї .

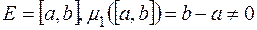Зясуємо зв'язок між лебеговим та невласним рімановим інтегралами.

Теорема. Нехай функція 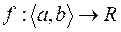визначена на проміжку , і задовольняє на ньому всім умовам, при яких можна вести мову про невласний ріманів інтеграл . Функція 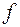буде інтегровною за Лебегом на проміжку 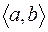тоді і лише тоді, коли вона абсолютно інтегровна на 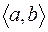за Ріманом у невласному розумінні тобто, коли існує невласний ріманів інтеграл

.

У випадку інтегровності функції 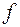за Лебегом на 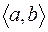виконується

.

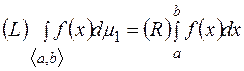Приклад. Як відомо з курсу математичного аналізу, інтеграл Діріхле

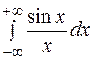
збігається лише умовно, як невласний ріманів інтеграл, тобто

.

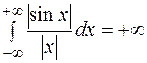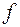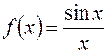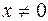Тому функція така, що при і 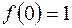не є інтегровною за Лебегом на .