Інтеграл за значенням Коші. Порівняння збіжності інтегралу за значенням Коші і невласного інтегралу

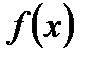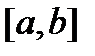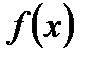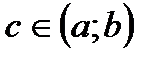Нехай функція визначена на . Припустимо, що для т. - особлива. Тоді, відповідно до лекції 39, маємо:

.

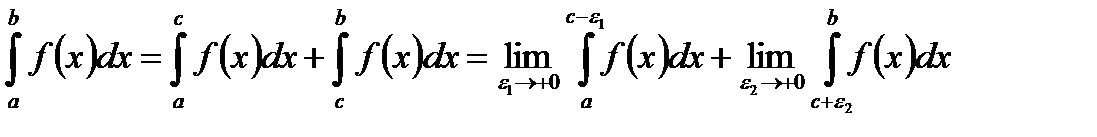Якщо не існує хоча б одна з цих границь, то НІ ІІ роду 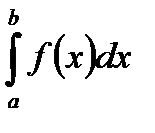є розбіжним. Тут 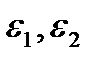- незалежні одне від одного.

Коші запропонував варіант, коли :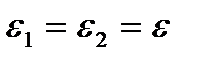

.

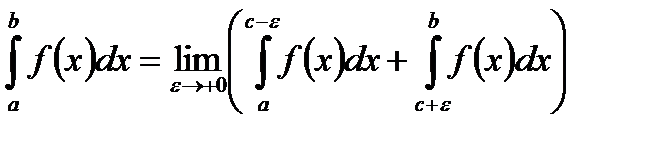При такому обчисленні 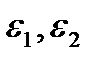вже не є незалежними – вони рівні. Такий спосіб обчислення не є загальним. Можливі такі випадки, що границі 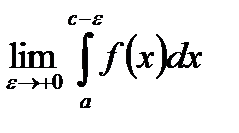, 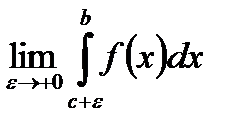окремо не існують, але існує границя суми 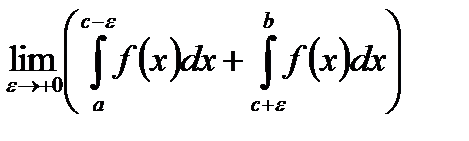. Тоді така границя називається головним значенням за Коші невластивого інтегралу (чи інтегралом за значенням Коші) і позначається

.

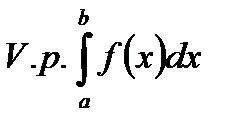Нехай 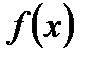визначена на 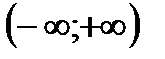, а НІ І роду

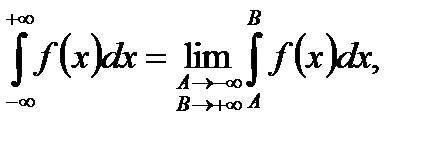
де 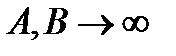незалежно одне від одного, розбігається. Але може статися, що якщо взяти симетричний проміжок, тобто 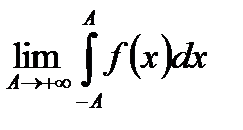, то вона буде існувати. Тоді ця границя називається НІ І роду за Коші і позначається:

.

Приклад. Розглянемо НІ І роду 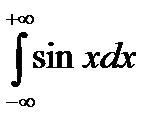. У класичному визначенні НІ І роду він є розбіжним, оскільки:

не існує.

Але

.

.

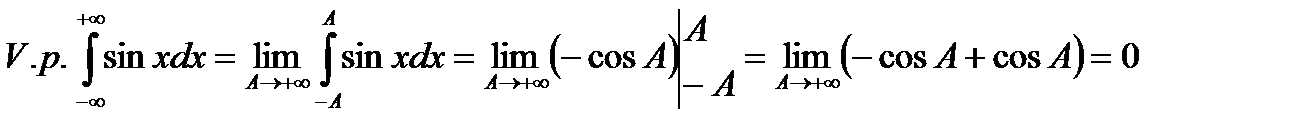Доцільність такого обчислення для розглянутого приклада стає очевидною з рис.1.

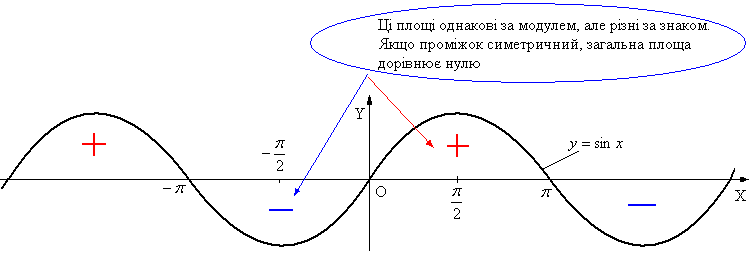
Рис.1.

Приклад. Розглянемо 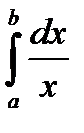, де 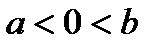. Цей НІ ІІ роду, як було зясовано в попередній лекції, розбігається. Обчислимо його значення за Коші:

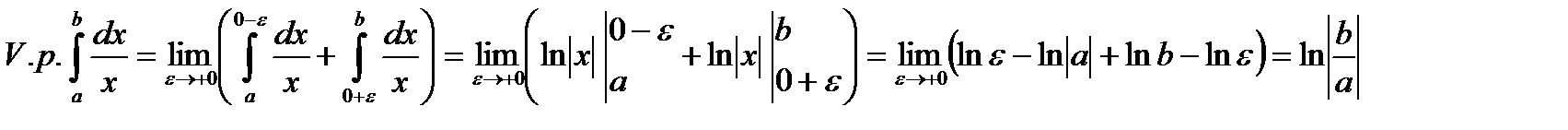
Таким чином, за Коші інтеграл 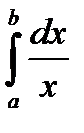є збіжним.

Приклад. Інтеграл 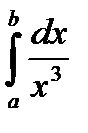, де 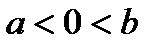, є розбіжним в класичному сенсі. Але

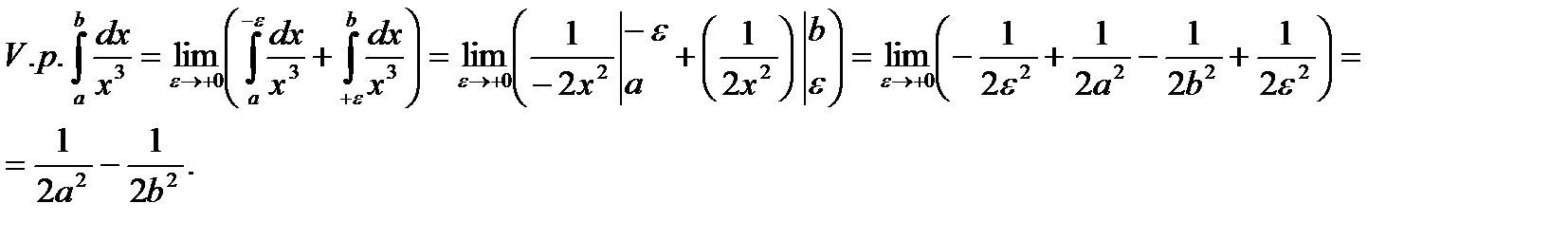
Твердження 1. Якщо функція 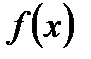визначена на і є непарною, то

,

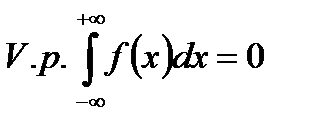а якщо 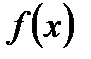- парна, то

.

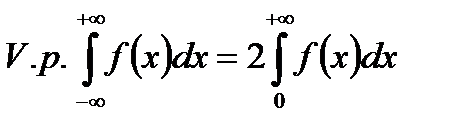Доказ. Нехай визначена на і є непарною. Тоді:

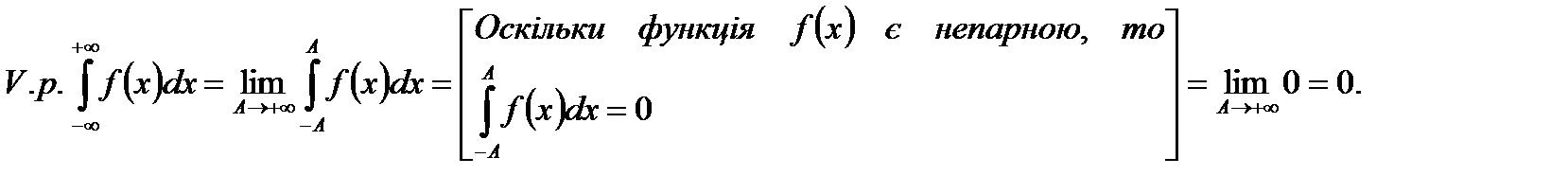
Аналогічно для парної функції.

Питання

1. Чи можна НІ ІІ роду звести до НІ І роду? Як саме?

2. Що таке інтеграл за значенням Коші?

3. У чому полягає сенс визначення НІ за значенням Коші?

4. Як визначається інтеграл за значенням Коші для парної функції?

5. Як визначається інтеграл за значенням Коші для непарної функції?