Компакти в просторі . Критерій компактності множини

План

1. Компакти в просторі 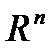. Критерій компактності множини
2. Теорема Больцано-Вейєрштрасса
3. Векторні послідовності. Поняття границі векторної послідовності
4. Найпростіші властивості границь векторних послідовностей
5. Фундаментальні послідовності. Підпослідовності

Компакти в просторі . Критерій компактності множини

Нехай подана сукупність 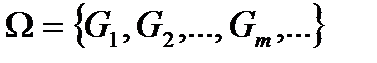відкритих множин у просторі .

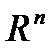Визначення 1. Кажуть, що сукупність множин 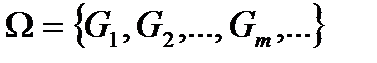покриває множину 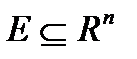, якщо .

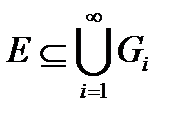Визначення 2. Множина 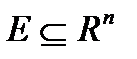називається компактною множиною, чи компактом, якщо з кожної нескінченної сукупності відкритих множин, яка покриває множину 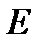, можливо добути скінченну сукупність, яка теж покриває множину .

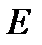Приклад. Нехай 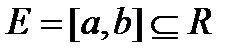. За лемою Бореля з кожної нескінченної системи інтервалів, яка покриває 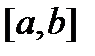, можна добути скінченну підсистему, яка покриває 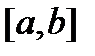, тому 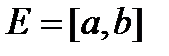- компакт.

Визначення 3. Замкненим паралелепіпедом в просторі 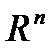називається множина точок 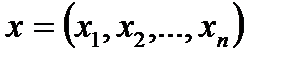, які задовольняють умовам:

.

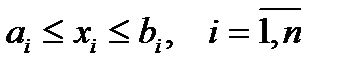Зауваження. Можливо показати, що замкнений паралелепіпед є компактом.

Визначення 4. Множина 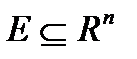називається обмеженою, якщо існує куля, яка містить цю множину.

Теорема 1. Для того, щоб множина 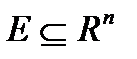була компактом, необхідно і достатньо, щоб вона була замкнена і обмежена.