В) в просторі

Для розв’язування головних геодезичних задач в просторі використовують системи просторових декартових (X, Y, Z), геодезичних (B, L, H) та топоцентричних горизонтальних - декартових (x’, y’,z’) та полярних (A, z,D) координат і зв’язки між ними (див. розділи 1 і 2).

Пряма геодезична задача формулюється наступним чином. Задані геодезичні координати B₁,L₁,H₁ початкової точки Q₁ і топоцентричні полярні координати z₁₂, A₁₂, D точки Q₂ відносно початкової точки Q₁. Необхідно визначити геодезичні координати B₂,L₂,H₂ точки Q₂.

Поставлену задачу розв’язують в такій послідовності:

а) за формулами зв’язку (2.32) обчислюють просторові декартові координати X₁,Y₁,Z₁ точки Q₁;

б) обчислюють елементи матриці перетворення координат A₁ за формулою (2.37).

в) використовуючи формули (2.34), обчислюють топоцентричні декартові координати x₂’,y₂’,z₂’;

г) за формулою (2.36) обчислюють декартові координати X₂,Y₂,Z₂ точки Q₂;

д) для переходу до геодезичних координат B₂,L₂,H₂ точки Q₂ використовують формули зв’язку (2.33).

Обернена геодезична задача . Задані геодезичні координати B,L,H двох точок Q₁ та Q₂. Необхідно знайти топоцентричні полярні координати z₁₂, A₁₂, D точки Q₂ відносно початкової точки Q₁.

Для розв’язування поставленої задачі можна застосувати таку схему:

а) від геодезичних координат B,L,H точок Q₁ та Q₂ за формулами (2.32) переходять до декартових X_i,Y_i,Z_i (де і=1,2);

б) обчислюють елементи транспонованої матриці перетворення координат 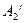за формулою

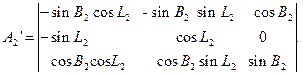
в) за формулою (2.38) обчислюють топоцентричні декартові координати x_i’,y_i’,z_i’ (і=1,2) точки Q₁ відносно точки Q₂ і навпаки.

г) топоцентричні полярні координати z₁₂, A₁₂, D точки Q₂ відносно початкової точки Q₁ і z₂₁, A₂₁, D точки Q₁ відносно точки Q₂ обчислюють за формулами (2.35).

Приведені вище схеми можна використовувати також і для розв’язування головної геодезичної задачі між точками на поверхні еліпсоїда. Для цього в цих формулах достатньо прийняти H₁=H₂=0. Розв’язком при цьому, наприклад, в оберненій геодезичній задачі будуть азимути прямого і оберненого нормальних перерізів та довжина хорди цих перерізів.