Розв’язування головних геодезичних задач

А) на поверхні сфери

Використання сфери вигідно, в першу чергу, для наближеного розв’язування головних геодезичних задач - прямої та оберненої.

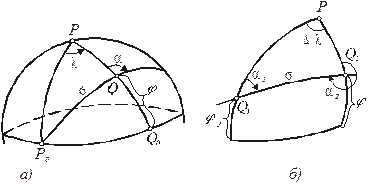
Введемо наступні позначення координат на сфері (рис.3.4):

j - географічна широта;

l - географічна довгота;

a - азимут дуги великого кола;

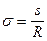Рис.3.4

Пряма геодезична задача

Нехай задані географічні координати j₁, l₁ деякої точки Q₁ (рис. 3.4б), а також полярні координати s і a₁ другої точки Q₂. Вимагається за цими даними знайти географічні координати j₂, l₂ точки Q₂ і азимут a₂ з другої точки на першу. Таким чином, пряма геодезична задача полягає в перетворенні полярних координат в географічні (сферичні).

Обернена геодезична задача.

Нехай задані географічні координати j₁, l₁ і j₂, l₂ двох точок Q₁ і Q₂ (рис. 3.4б). Необхідно знайти найкоротшу відстань s (довжину дуги великого кола) між даними точками та азимути a₁ і a₂ з однієї точки на другу. Отже, обернена геодезична задача зводиться до перетворення географічних (сферичних) координат в полярні.

Розв’язування прямої і оберненої геодезичних задач на сфері, як легко можна побачити, представляє собою розв'язування полярного сферичного трикутника Q₁PQ₂ (рис.3.4б). В даному випадку розв'язування цього трикутника зводиться до визначення за двома сторонами і кутом між ними третьої сторони та прилеглих до неї кутів. Для розв'язування можна використати замкнуті формули сферичної тригонометрії:

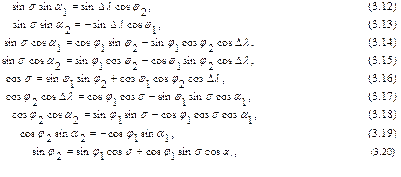
Формули для розв’язування прямої геодезичної задачі:

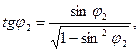(3.21)

де 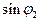визначається за формулою (3.20). Різниця довгот Dl знайдеться, якщо розділити рівняння (3.12) на (3.17)

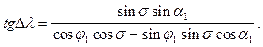(3.22)

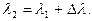
Шляхом ділення рівнянь (3.19) на (3.18) дістанемо формулу для оберненого азимута

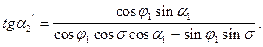(3.23)

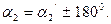
Формули для розвязування оберненої геодезичної задачі:

Для обчислення прямого азимута треба розділити рівняння (3.12) на (3.14)

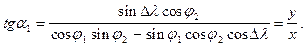(3.24)

Для обчислення оберненого азимута необхідно розділити рівняння (3.13) на (3.15)

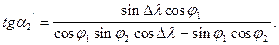(3.25)

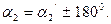
Формулу для sins отримаємо, якщо помножимо рівняння (3.12) на sina₁, а рівняння (3.14) - на cosa₁ і додамо їх

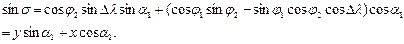(3.26)

Обчислення арксинуса можна замінити обчисленням арктангенса, використавши формулу зв’язку, аналогічну (3.21).

Із трикутника Q₁ PQ₂ (див. рис. 3.4.б) можна отримати і інші варіанти формул для розв’язування прямої та оберненої геодезичних задач.