Диференційні формули для довільної точки простору.

Встановимо залежності між малими змінами просторових декартових і геодезичних координат довільної точки в просторі. В загальному вигляді ці залежності можна записати

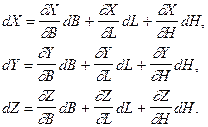(3.44)

Часткові похідні в цих залежностях можна знайти із рівнянь (2.32)

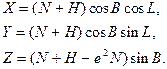(3.45)

Для цього попередньо визначимо похідні двох функцій

Враховуючи, що

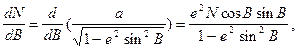
а радіус кривини меридіана M можна записати у вигляді

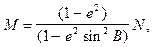
то для наведених функцій матимемо

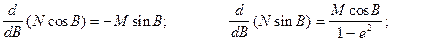
Після цього можна легко знайти часткові похідні, наприклад

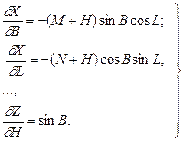(3.46)

Після підстановки похідних в попередні залежності, отримаємо

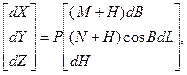(3.47)

де матриця перетворення P має елементи

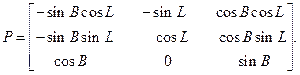(3.47¢)

Звідси можна знайти і обернені залежності

(3.48)

де 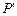- транспонована матриця Р.