Диференційні формули для геодезичної лінії.

Сім змінних B₁, L₁, B₂, L₂, s, A₁, A₂ геодезичної лінії зв’язані між собою складною залежністю, котра визначається формулами розв’язування головних геодезичних задач. З цих семи змінних чотири є незалежними; від них залежать решта три.

Зміну трьох залежних змінних представимо у вигляді повних диференціалів

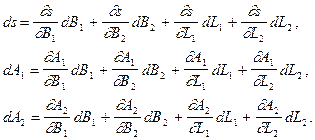(3.37)

Ці рівняння показують, як змінюється довжина геодезичної лінії та її азимути у випадку, якщо кінці цієї лінії отримують деякі малі зміщення, котрі виражені диференціалами координат. Рівняння (3.37) приймаються за вихідні співвідношення, з яких потім знаходять інші залежності між цими диференціалами.

Часткові похідні можна знайти, застосовуючи при цьому два підходи. Перший - менш строгий- полягає в тому, що при виводі формул користуються геометричним представленням часткових диференціалів, що складають праві частини рівнянь (3.37), а другий - строгий - в тому, що часткові похідні знаходять диференціюванням за відповідними змінними рівнянь, що використовують для розв’язування головних геодезичних задач. В курсах вищої геодезії [1,5,7] ці підходи розглядаються детальніше. Ми обмежимося лише готовими формулами, які будемо класифікувати за впливами:

¨ зміни широти B₂ на величини s, A₁, A₂ при постійній величині довготи L₂ та незмінному положенні початкової точки Q₁

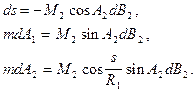(3.38)

Тут m - приведена довжина геодезичної лінії. Для більшості випадків її можна обчислити за формулою: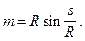

¨ зміни довготи L₂ на величини s, A₁, A₂ при постійній величині широти B₂ та незмінному положенні початкової точки Q₁

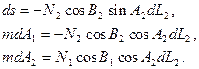(3.39)

Аналогічні вирази будуть і в тому випадку, коли кінцева точка Q₂ залишається в незмінному положенні, а зміщення отримала початкова точка Q₁ . Різниця буде лише в тому, що у формулах (3.38) та (3.39) поміняються місцями індекси 1 і 2. Повні диференційні формули запишуться в цьому випадку в наступному виді

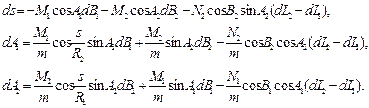(3.40)

· зміни широти B₁ на величини B₂, L₂, A₂ при постійній величині довготи L₁ , азимута A₁ та довжини геодезичної лінії s

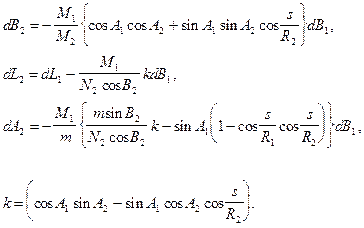(3.41)

· зміни довжини геодезичної лінії s на величини B₂, L₂, A₂ при постійній величині широти B₁, довготи L₁ , азимута A₁

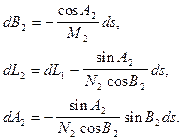(3.42)

· зміни азимута A₁ на величини B₂, L₂, A₂ при постійній величині широти B₁, довготи L₁ тадовжини геодезичної лінії s

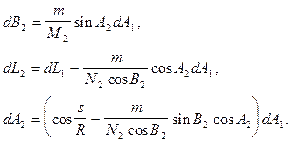(3.43)

Рис. 3.5 дає геометричне представлення про величини, що входять в диференційні формули (3.38)- (3.43).

Рис. 3.5

Всі наведені вище формули є наближеними, поскільки в них не прийняті до уваги диференціали другого і більш вищих порядків. Тому вони тим точніші, чим менші величини диференціалів незалежних змінних.