Паралельні прямі у просторі
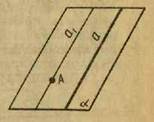
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються. Прямі, що не перетинаються і не лежать в одній площині, називаються мимобіжними (рис. 11).
Теорема 2.1. Через точку, що не лежить на даній прямій, можна провести пряму, паралельну цій прямій, і тільки одну.
Зауваження. Твердження єдиності в теоремі 2.1 не є простим наслідком аксіоми паралельних, тому що цією аксіомою стверджується єдиність прямої, паралельної даній в даній площині. Тому це твердження вимагає доведення.
Доведення. Нехай а — дана пряма і А — точка, що не лежить на цій прямій (рис. 12). Проведемо через пряму а і точку А площину α. Проведемо через точку А в площині α пряму а1 паралельну а. Доведемо, що пряма а1, паралельна а, єдина.
Допустимо, що існує інша пряма а2, яка проходить через точку А і паралельна прямій а. Через прямі а і а2 можна провести площину α2.
Площина α2 проходить через пряму а і точку А; тому по теоремі 1.1 вона збігається з α. Тоді по аксіомі паралельних прямі а1 і а2 збігаються. Теорема доведена.
 | |||
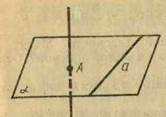 | |||
Мал. 11 Мал. 12
Дата добавления: 2015-08-26; просмотров: 1281;
