Ознака паралельності прямих
Теорема 2.2. Дві прямі, паралельні третій прямій, паралельні.
Доведення. Нехай прямі b і с паралельні прямій а. Доведемо, що прямі b і с паралельні.
Випадок, коли прямі а, b, с лежать в одній площині, був розглянутий у планіметрії. Тому припустимо, що наші прямі не лежать в одній площині. Нехай β - площина, в якій лежать прямі а і b, а γ - площина, у якій лежать прямі аіс. Площини β і γ різні (рис. 13). Візьмемо на прямій b довільну точку В и проведемо площину γ1 через пряму с і точку В. Вона перетне площину β по прямій b1.
Пряма b1 не перетинає площину γ. Дійсно, точка перетину повинна належати прямій а, тому що пряма b1 лежить у площині β. З іншого боку, вона повинна лежати на прямій с, оскільки пряма b1 лежить у площині γ1. Але прямі а і с як паралельні не перетинаються.
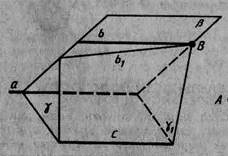Оскільки пряма b1 лежить у площині β і не перетинає пряму а, то вона паралельна прямій а, а отже, збігається з b за аксіомою паралельних. Таким чином, пряма b, збігаючись з прямою b1, лежить в одній площині з прямою с (у площині γ1) і не перетинає її. Виходить, прямі b і с паралельні. Теорему доведено.
Мал. 13
Дата добавления: 2015-08-26; просмотров: 930;