Ознака паралельності площин
Дві площини називаються паралельними, якщо вони не перетинаються.
Теорема 2.4. Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.
Доведення. Нехай α иβ — дані площини, а1 і а2 - дві прямі в площині α, що перетинаються в точці А, b1 і b2 відповідно паралельні їм прямі в площині β (мал. 15).
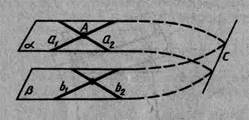Припустимо, що площини α иβ не паралельні, тобто перетинаються по якій-небудь прямій с. По теоремі 2.3 прямі а1 і а2, які паралельні прямим b1 і b2, паралельні площини β, і тому вони не перетинають пряму с, що лежить у цій площині. Таким чином, у площині α через крапку А проходять дві прямі (а1 і а2), паралельні прямій с. Але це неможливо за аксіомою паралельності. Ми прийшли до суперечності. Теорема доведена.
Мал. 15
Дата добавления: 2015-08-26; просмотров: 2321;