РОЗВ’ЯЗАННЯ ЗАДАЧ НА ПАРАЛЕЛЬНІСТЬ

1. Доведіть, що коли прямі АВ і СD мимобіжні, то прямі АС і ВD також мимобіжні.

2. Можна чи через точку С, яка не належить мимобіжним прямим а і b, провести дві різні прямі, кожна з яких перетинає прямі а і b? Відповідь поясніть.

3. Доведіть, що всі прямі, що перетинають дві дані паралельні прямі, лежать в одній площині.

4. Прямі а і b перетинаються. Доведіть, що всі прямі, які паралельні прямій b і перетинають пряму а, лежать в одній площині.

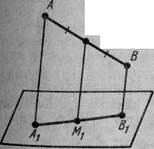
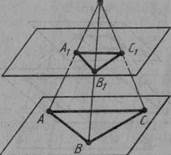
5. Через кінці відрізка АВ і його середину М проведено паралельні прямі, що перетинають деяку площину в точках А₁, В₁ і М₁. Знайдіть довжину відрізка ММ₁, якщо відрізок АВ не перетинає площину (рис. 20) і якщо:
1) АА₁ = 5м, ВВ₁ = 7м; 2) АА₁ =3,6 дм, ВВ₁=4,8дм;

3) АА₁= 8,3 см, ВВ₁ = 4,1 см; 4) АА₁ =а, ВВ₁ = b.

6.* Розв'яжіть попередню задачу за умови, що відрізок АВ перетинає площину.

Мал. 20 Мал. 21

7. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, що перетинають площину в точках В₁ і С₁. Знайдіть довжину відрізка ВВ₁, якщо: 1) СС₁ = 15 см, АС:ВР = = 2:3; 2) СС₁= 8,1 см, АВ:АС = 11:9; 3) АВ=6 см, АС : СС₁ = 2:5; 4) АС = а, ВР = b, СС₁= с.

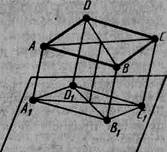
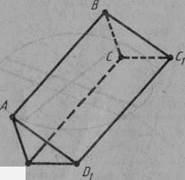
8*. Дано паралелограм АВСD і площину, яка не перетинає його. Через вершини паралелограма проведено паралельні прямі, які перетинають дану площину в точках А₁, В₁, С₁, D₁ (рис.21). Знайдіть довжину відрізка DD₁, якщо: 1) АА₁ = 2м, ВВ₁=3м, СС₁=8м; 2) АА₁=4м, ВВ₁=3_М, СС₁ = 1 м; 3) АА₁= а, ВВ₁ = b, СС₁ = с.

9. Прямі а і b не лежать в одній площині. Чи можна провести пряму с, паралельну прямим а і b?

10. Точки А, В, С, D не лежать в одній площині. Доведіть, що пряма, що проходить через середини відрізків АВ і ВС, паралельна прямій, яка проходить через середини відрізків АD і СD.

11.Доведіть, що середини сторін просторового чотирикутника є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині).

12.Дано чотири точки А, В, С, D, які не лежать в одній площині. Доведіть, що прямі, що з'єднують середини відрізків АВ і СD, АС і ВD, АD і ВС, перетинаються в одній точці.

13. Дано трикутник АВС. Площина, паралельна прямій АВ, перетинає сторону АС цього трикутника в точці А₁, а сторону ВС — у точці В₁. Знайдіть довжину відрізка А₁В₁ якщо: 1) АВ = 15 см, АА₁:АС = 2:3; 2) АВ = 8 см, АА₁ : А₁С = 5:3; 3) В₁С = 10 см, АВ : ВР = 4:5; 4) АА₁=а, АВ= b, А₁С = с.

14 Через дану точку проведіть пряму, паралельну кожній з двох даних площин, які перетинаються.

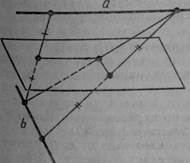
15. Доведіть, що коли площина перетинає одну з двох паралельних прямих, то вона перетинає й другу.

16. Доведіть, що через будь-яку з двох мимобіжних прямих можна провести площину, паралельну другій прямій.

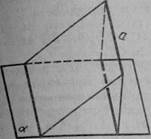
17. Доведіть, що коли дві площини, які перетинаються по прямій а, перетинають площину α по паралельних прямих, то пряма а паралельна площині α (рис. 22).

18. Доведіть, що коли пряма перетинає одну із двох паралельних площин, то вона перетинає й другу.

19. Доведіть, що через дві мимобіжні прямі можна провести паралельні площини.

20. Через дану точку простору проведіть пряму, яка перетинає кожну із двох мимобіжних прямих (рис. 23). Чи завжди це можливо?

21.Доведіть, що геометричне місце середин відрізків з кінцями на двох мимобіжних прямих є площина, паралельна цим прямим (рис. 24).

22. Дано чотири точки А, В, С, D, які не лежать в одній площині. Доведіть, що будь-яка площина, паралельна прямим АВ і СD, перетинає прямі АС, АD, ВD і ВС у вершинах паралелограма (рис. 25).

23. Площини α і β паралельні площини γ. Чи можуть площини α і β перетинатись?

24. Площини α і β перетинаються. Доведіть, що будь-яка площина γ перетинає хоча б одну з площин α і β.

25. Доведіть, що усі прямі, які проходять через дану точку паралельно даній площині, лежать в одній площині.

26. Через дану точку проведіть площину, паралельну кожній з двох прямих, які перетинаються. Чи завжди це можливо?

27. Паралелограми АВСD і АВС₁D₁ лежать у різних площинах. Доведіть, що чотирикутник СDD₁С₁ також паралелограм (рис. 26).

28. Через вершини паралелограма АВСD, що лежить в одній з двох паралельних площин, проведено паралельні прямі, які перетинають іншу площину в точках А₁, В₁, С₁, D₁. Доведіть, що чотирикутник А₁В₁С₁D₁ також паралелограм.

29. Через вершини трикутника АВС, що лежить в одній з двох паралельних площин, проведено паралельні прямі, які перетинають другу площину в точках А₁, В₁, С₁. Доведіть рівність трикутників АВС і А₁В₁С₁.

30. Три прямі, які проходять через одну точку, перетинають дану площину в точках А, В, С, а паралельну їй площину в точках А₁, В₁, С₁. Доведіть подібність трикутників АВС і А₁В₁С₁(рис. 27).

31. Доведіть, що коли чотири прямі, які проходять через точку А, перетинають площину α у вершинах паралелограма, то вони перетинають будь-яку площину, яка паралельна α і не проходить через точку А, теж у вершинах паралелограма (рис. 28).

32. Дано дві паралельні площини. Через точки А и В одній із площин проведені паралельні прямі, що перетинають другу площину в точках А₁, В₁. Чому дорівнює відрізок А₁В₁, якщо АВ = а?

33.Дано дві паралельні площини α₁ і α₂ і точка А, яка не лежить в жодній з цих площин. Через точку А проведено довільну пряму. Нехай Х₁ і X₂ — точки перетину її з площинами α₁ і α₂. Доведіть, що відношення довжин відрізків АХ₁: АХ₂ не залежить від узятої прямої.

34. Дано чотири паралельні прямі. Доведіть, що коли яка-небудь площина перетинає ці прямі у вершинах паралелограма, то будь-яка площина, не паралельна даним прямим, перетинає їх у вершинах деякого паралелограма.

35. Дано паралельну проекцію трикутника. Як побудувати проекції медіан цього трикутника?

Мал. 22 Мал. 23 Рис. 24

Мал. 25 Мал. 26 Мал. 27

Мал. 28