ПЕРЕПЕНДИКУЛЯРНОСТЬ ПРЯМИХ І ПЛОЩИН
План
- Перпендикулярність прямих і площин.
- Ознака перпендикулярності прямої і площини
- Властивості прямої і площини, перпендикулярних між собою
- Перпендикуляр і похила
- Теорема про три перпендикуляри
- Перпендикулярність прямих і площин
Як і на площині, дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Теорема 3.1. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони також перпендикулярні.
Доведення. Нехай а й b — перпендикулярні прямі, а1 і b1 — паралельні їм прямі, які перетинаються. Доведемо, що прямі а1 і b1 перпендикулярні.
Якщо прямі а, b, а1, b1 лежать в одній площині, то вони мають зазначену в теоремі властивість, яка відома із планіметрії.
Припустимо тепер, що наші прямі не лежать в одній площині. Тоді прямі а і b лежать у деякій площині α, а прямі а1 і b1 — у якійсь площині α1 (мал. 33). По теоремі 2.4 площини α і α1 паралельні. Нехай С — точка перетину прямих, а і b, а С1 — точка перетину прямих а1 і b1. Проведемо в площині паралельних прямих а і а1 пряму, паралельну прямій СС1. Вона перетне прямі а і а1 у крапках А и А1. У площині прямих b і b1 проведемо пряму, паралельну прямій СС1, і позначимо через В и В1 точки її перетину з прямими b і b1.
Чотирикутники САА1С1 і СВВ1С1-паралелограми, тому що у них протилежні сторони паралельні. Чотирикутник АВВ1А1 — також паралелограм. У нього сторони АА1, ВВ1 паралельні, тому що кожна з них паралельна прямій СС1.
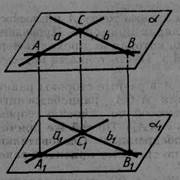 Таким чином, чотирикутник лежить у площині, що проходить через паралельні прямі АА1 і ВВ1. А вона перетинає паралельні площини α і α1 попаралельним прямим АВ і А1В1.
Таким чином, чотирикутник лежить у площині, що проходить через паралельні прямі АА1 і ВВ1. А вона перетинає паралельні площини α і α1 попаралельним прямим АВ і А1В1.
Тому що у паралелограма протилежні сторони рівні, то АВ = А1В1, АС = А1С1, ВС=В1С1. За третьою ознакою рівності трикутників трикутники АВС і А1В1С1 рівні. Отже, кут А1С1В1, який дорівнює куту АСВ, прямий, тобто прямі а1 і b1 перпендикулярні. Теорема доведена.
Мал. 33
- Ознака перпендикулярності прямій і площини
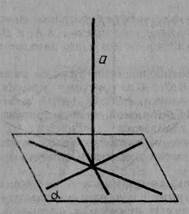
Пряма, що перетинає площину, називається перпендикулярноюдо цієї площини, якщо вона перпендикулярна будь-який прямій, що лежить у цій площині і проходить через точку перетину (мал. 34).
Теорема 3.2. Якщо пряма перпендикулярна до двох прямих, що лежать у площині і перетинаються, то вона перпендикулярна до даної площини.
Доведення. Нехай а — пряма, перпендикулярна прямим b іс у площині α.
Тоді пряма а проходить через точку А перетину прямих b іс(мал. 35). Доведемо, що пряма а перпендикулярна площини α.
Проведемо довільну пряму х через точку А в площини α і покажемо, що вона перпендикулярна прямій а. Проведемо в площині α довільну пряму, яка не проходить через точку А и перетинає прямі b, с і х. Нехай точками перетинання будуть В, С и X.
Відкладемо на прямій а від точки А в різні сторони рівні відрізки: АА1 і АА2. Трикутник А1СА2 рівнобедрений, оскільки відрізок АС є висотою за умовою теореми і медіаною — по побудові (АА1 =АА2). З тієї ж причини трикутник А1ВА2 також рівнобедрений. Отже, трикутники А1ВС і А2ВС рівні за третьою ознакою рівності трикутників.
З рівності трикутників А1ВС і А2ВС випливає рівність кутів А1ВХ, А2ВХ і, виходить, рівність трикутників А1ВХ і А2ВХ за першою ознакою рівності трикутників. З рівності сторін А1Х и А2Х цих трикутників робимо висновок, що трикутник А1ХА2 рівнобедрений. Тому його медіана ХА є також висотою. А це значить, що пряма х перпендикулярна до а. За означенням пряма а перпендикулярна площини α. Теорема доведена.
 |  | ||
Мал. 34 Мал. 35
Задача. Доведіть, що через дану точку прямої можна провести одну і тільки одну перпендикулярну до неї площину.
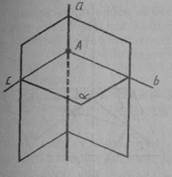
Розв’язання. Нехай а — дана пряма і А — точка на ній (мал. 36). Проведемо через неї дві площини, а в них — через точку А прямі b і с, перпендикулярні до прямої а. Площина α, що проходить через ці прямі, перпендикулярна до прямої а по теоремі 3.2.
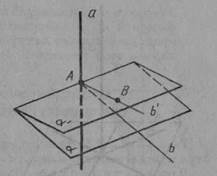
Доведемо, що ця площина єдина. Припустимо, що крім площини α існує інша площина α', що проходить через точку А и перпендикулярна до прямої а (мал. 37). Нехай В — точка площини α', що не лежить у площині α. Проведемо через точку В і пряму а площину. Вона перетне площини α і α' по різним прямим b і b', що перпендикулярні до прямої а. А це, як ми знаємо, неможливо, оскільки на площині через дану точку прямої проходить тільки єдина перпендикулярна до неї пряма. Отже, площина, що проходить через точку А і перпендикулярна до прямої а, єдина.
 |  | ||
Мал. 36 Мал. 37
Задача. Доведіть, що через дану точку площини можна провести одну й тільки одну перпендикулярну до неї пряму.
Розв’язання. Нехай α — дана площина і А — точка на ній (мал. 38). Проведемо в площині α через точку А дві прямі b і с. Проведемо через точку А перпендикулярні до них площини. Вони перетнуться по деякої прямій а, перпендикулярної прямим b і с. Отже, пряма а перпендикулярна площини α.
Доведемо, що ця пряма єдина. Припустимо, що крім прямої а існує інша пряма а', що проходить через точку А і перпендикулярна площини α (мал. 39). Проведемо через прямі а і а' площину. Вона перетне площину α по деякій прямій b, перпендикулярній до прямих а і а'. А це неможливо. Отже, пряма, що проходить через дану точку площини і перпендикулярна до цієї площини, єдина.
 | 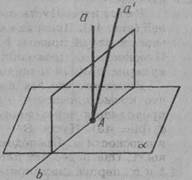 |
Мал. 38 Мал. 39
- Властивості прямої і площини, перпендикулярних між собою
Теорема 3.3. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
Доведення. Нехай а1, і а2 — дві паралельні прямі й α - площина, перпендикулярна прямій а1 (мал. 40). Доведемо, що ця площина перпендикулярна і прямій а2.
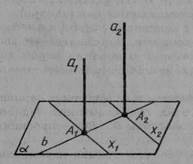 Проведемо через точку А2 перетину прямій а2 з площиною α довільну пряму х2 у площині α. Проведемо в площині α через точку А1 перетину прямої а1 з α пряму х1, паралельну прямій х2. Оскільки пряма а1 перпендикулярна до площини α, то прямі а1 і х1 перпендикулярні. А за теоремою 3.1 паралельні до них прямі а2 і х2 , що перетинаються, також перпендикулярні. Таким чином, пряма а2 перпендикулярна до будь-якої прямої х2 у площині α. А це значить, що пряма а2 перпендикулярна до площини α. Теорема доведена.
Проведемо через точку А2 перетину прямій а2 з площиною α довільну пряму х2 у площині α. Проведемо в площині α через точку А1 перетину прямої а1 з α пряму х1, паралельну прямій х2. Оскільки пряма а1 перпендикулярна до площини α, то прямі а1 і х1 перпендикулярні. А за теоремою 3.1 паралельні до них прямі а2 і х2 , що перетинаються, також перпендикулярні. Таким чином, пряма а2 перпендикулярна до будь-якої прямої х2 у площині α. А це значить, що пряма а2 перпендикулярна до площини α. Теорема доведена.
Мал. 40
Теорема 3.4. Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні.
Доведення. Нехай а і b — дві прямі, перпендикулярні до площини α (мал. 41).
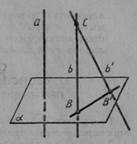 Припустимо, що прямі а і b не паралельні. Оберемо на прямій b точку С, що не лежить на площині α.
Припустимо, що прямі а і b не паралельні. Оберемо на прямій b точку С, що не лежить на площині α.
Проведемо через точку С пряму b', паралельну прямій а. Пряма b' перпендикулярна до площини α (теорема 3.3). Нехай В и В' — точки перетину прямих b і b' з площиною α. Тоді пряма ВВ' перпендикулярна до прямих b і b', що перетинаються. А це неможливо. Ми прийшли до суперечності. Теорема доведена.
Мал. 41
- Перпендикуляр і похила
Нехай дано площину і точка, яка не лежить на ній.
Перпендикуляром, опущеним з даної точки на дану площину, називається відрізок, що з'єднує дану точку із точкою площини і лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, що лежить у площині, називається основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину.
Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, що з'єднує дану точку із точкою площини і не є перпендикуляром до площини. Кінець відрізка, що лежить у площині, називається основою похилої. Відрізок, що з'єднує основи перпендикуляра і похилої, проведених з однієї й тієї ж точки, називається проекцією похилої.
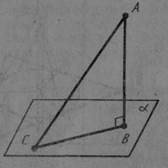 |
На малюнку 42 із точки А проведені до площини α перпендикуляр АВ і похила АС. точка В — основа перпендикуляра, точка С — основа похилої, ВС — проекція похилої АС на площину α.
Мал. 42
Дата добавления: 2015-08-26; просмотров: 3042;
