Відстанню між паралельними площинами називається відстань від будь-якої точки однієї площини до іншої площини.
- Теорема про три перпендикуляри
Теорема 3.5. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої. І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Доведення. Нехай АВ — перпендикуляр до площини α, АС — похила і с — пряма в площині α, що проходить через основу С похилої (мал. 43). Проведемо пряму СА', паралельну прямій АВ. Вона перпендикулярна до площини α.
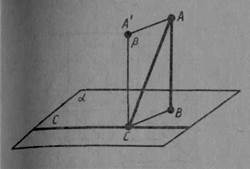 Проведемо через прямі АВ і А'С площину β. Пряма с перпендикулярна до прямої СА'. Якщо вона перпендикулярна до прямої СВ, то вона перпендикулярна і до площини β, а отже, і до прямої АС.
Проведемо через прямі АВ і А'С площину β. Пряма с перпендикулярна до прямої СА'. Якщо вона перпендикулярна до прямої СВ, то вона перпендикулярна і до площини β, а отже, і до прямої АС.
Аналогічно, якщо пряма с перпендикулярна до похилої СА, то вона, як перпендикуляр і до прямої СА', перпендикулярна до площини β, а отже, і до проекції похилої ВС. Теорема доведена.
Мал. 43
Дата добавления: 2015-08-26; просмотров: 1537;
