Канторові множини
Сегмент 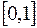 точками
точками 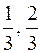 розділимо на 3 частини однакової довжини. Вилучивши із сегмента
розділимо на 3 частини однакової довжини. Вилучивши із сегмента 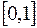 середній інтервал
середній інтервал 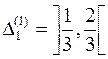 , дістанемо об’єднання двох сегментів
, дістанемо об’єднання двох сегментів 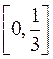 ,
, 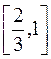 . Сегмент
. Сегмент  точками
точками 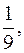
 , а сегмент
, а сегмент  точками
точками 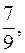
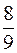 розділимо знову на три частини однакової довжини. Вилучивши із вказаних сегментів середні інтервали
розділимо знову на три частини однакової довжини. Вилучивши із вказаних сегментів середні інтервали
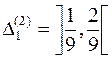 ,
, 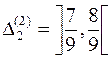 дістанемо об’єднання 4 сегментів
дістанемо об’єднання 4 сегментів 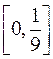 ,
, 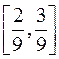 ,
,  ,
, 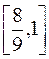 . Кожен із останніх сегментів знову розділимо на 3 частини однакової довжини і вилучимо середні інтервали. І так далі. Продовжуючи цей процес до нескінченності, дістанемо певну множину
. Кожен із останніх сегментів знову розділимо на 3 частини однакової довжини і вилучимо середні інтервали. І так далі. Продовжуючи цей процес до нескінченності, дістанемо певну множину 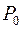 , що утворюється із
, що утворюється із 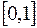 шляхом вилучення з нього зчисленної сукупності інтервалів
шляхом вилучення з нього зчисленної сукупності інтервалів 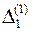 ,
, 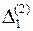 ,
, 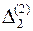 , … Множина
, … Множина 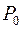 називається канторовою множиною. Множина
називається канторовою множиною. Множина 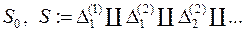 , також називається канторовою множиною. Очевидно,
, також називається канторовою множиною. Очевидно, 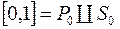 . Зрозуміло, що множина
. Зрозуміло, що множина 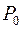 не включає жодного сегмента як завгодно малої довжини. Множина
не включає жодного сегмента як завгодно малої довжини. Множина 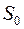 є відкрита, як об’єднання зчисленної сукупності інтервалів, що попарно не перетинаються. Тому множина
є відкрита, як об’єднання зчисленної сукупності інтервалів, що попарно не перетинаються. Тому множина 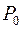 є замкнута, як доповнення відкритої множини
є замкнута, як доповнення відкритої множини 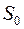 до сегмента
до сегмента 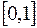 . Оскільки множини
. Оскільки множини 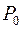 та
та 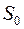 є відповідно замкнута і відкрита , то вони вимірні за Лебегом, як множини на числовій прямій.
є відповідно замкнута і відкрита , то вони вимірні за Лебегом, як множини на числовій прямій.
Множина 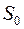 є об’єднання 1 інтервала першого рангу
є об’єднання 1 інтервала першого рангу 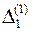 (який вилучається із
(який вилучається із 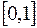 на першому кроці його поділу), двох інтервалів другого рангу
на першому кроці його поділу), двох інтервалів другого рангу 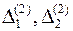 (які викидаються із сегментів
(які викидаються із сегментів  ,
,  на другому кроці при їх поділу) і т. д. Оскільки множина
на другому кроці при їх поділу) і т. д. Оскільки множина 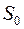 включає
включає 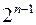 інтервалів n-го рангу, довжина кожного з яких дорівнює
інтервалів n-го рангу, довжина кожного з яких дорівнює 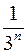 , то лінійна міра Лебега множини
, то лінійна міра Лебега множини 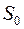 обчислюється наступним способом
обчислюється наступним способом
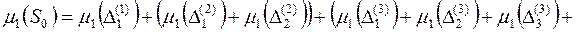
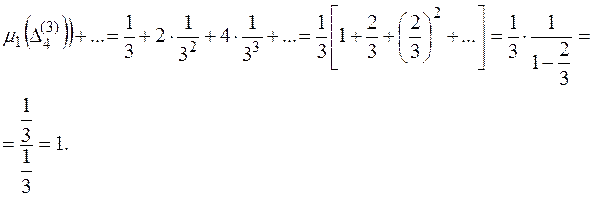 Оскільки
Оскільки 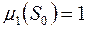 , то
, то 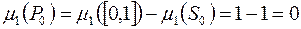 . Таким чином канторова множина
. Таким чином канторова множина 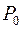 має лебегову міру рівну нулю,
має лебегову міру рівну нулю, 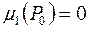 .
.
До множини 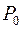 належать всі кінці вилучених із
належать всі кінці вилучених із 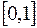 інтервалів. Тому ця множина не менш ніж зчисленна за потужністю. Однак, справедливе наступне твердження.
інтервалів. Тому ця множина не менш ніж зчисленна за потужністю. Однак, справедливе наступне твердження.
Теорема. Множина Кантора 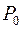 має потужність континуума.
має потужність континуума.
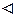 Припустимо протилежне до твердження теореми тобто, що множина
Припустимо протилежне до твердження теореми тобто, що множина 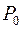 є зчисленна. Тоді її можна записати у вигляді
є зчисленна. Тоді її можна записати у вигляді
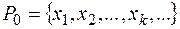 , де
, де 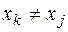 при
при 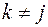 . (1)
. (1)
Позначимо через 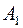 той із двох сегментів першого рангу
той із двох сегментів першого рангу  ,
,  , який не містить точку
, який не містить точку 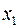 ,
, 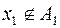 ; позначимо через
; позначимо через 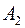 , той із чотирьох сегментів другого рангу, що включаються в
, той із чотирьох сегментів другого рангу, що включаються в 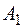 , який не містить точку
, який не містить точку 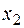 ,
, 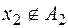 . І так далі.
. І так далі.
Продовжуючи цей процес до нескінченності, дістанемо послідовність сегментів 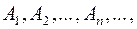 таку, що
таку, що 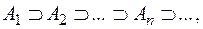 і при цьому
і при цьому 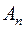 не містить точок
не містить точок 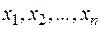 . Оскільки крім того
. Оскільки крім того 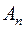 має довжину
має довжину 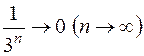 , то згідно з лемою про стяжні сегменти, сегменти послідовності
, то згідно з лемою про стяжні сегменти, сегменти послідовності 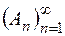 мають і причому єдину спільну точку
мають і причому єдину спільну точку 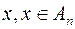
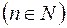 , яка не є елементом послідовності (1), що суперечить нашому припущенню. Одержане протиріччя і показує справедливість теореми.
, яка не є елементом послідовності (1), що суперечить нашому припущенню. Одержане протиріччя і показує справедливість теореми.
Зауваження. Із доведеної теореми випливає, що канторова множина 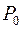 окрім кінців інтервалів, що вилучаються із
окрім кінців інтервалів, що вилучаються із 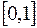 при її утворенні, містить ще й інші точки, бо в протилежному випадку вона була б лише зчисленною.
при її утворенні, містить ще й інші точки, бо в протилежному випадку вона була б лише зчисленною.
Дата добавления: 2015-07-24; просмотров: 1124;
