Стандартне продовження міри із півкільця на -алгебру.
Нагадаємо, що функція 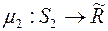 , називається продовженням (поширенням) функції
, називається продовженням (поширенням) функції 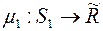 із класу множин
із класу множин 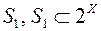 , на клас множин
, на клас множин 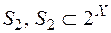 , якщо
, якщо 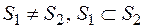 і
і 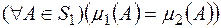 . При цьому функція
. При цьому функція 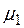 називається звуженням функції
називається звуженням функції 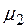 із класу
із класу 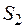 на клас
на клас 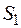 і пишуть
і пишуть 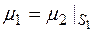 .
.
Якщо дано міру 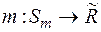 , визначену на півкільці
, визначену на півкільці 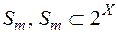 , то зразу ж виникає питання про можливість продовження її з півкільця
, то зразу ж виникає питання про можливість продовження її з півкільця 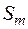 на більш широкий клас множин.
на більш широкий клас множин.
Теорема1. Міра 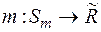 , яка визначена на півкільці
, яка визначена на півкільці 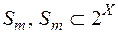 , завжди може бути продовжена причому єдиним способом із півкільця
, завжди може бути продовжена причому єдиним способом із півкільця 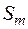 до міри визначеної на кільці
до міри визначеної на кільці 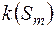 і таке продовження здійснює міра
і таке продовження здійснює міра 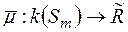 , яка задається за допомогою формули
, яка задається за допомогою формули
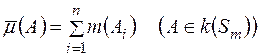 , (1)
, (1)
де 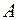 - довільна множина з
- довільна множина з 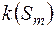 , що записана у вигляді
, що записана у вигляді
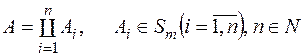 , (2)
, (2)
тобто при вказаних умовах 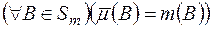 . При цьому міра
. При цьому міра 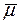 скінченна (
скінченна ( 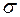 -скінченна), якщо міра
-скінченна), якщо міра 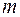 скінченна (
скінченна ( 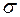 -скінченна).
-скінченна).
 Спочатку зазначимо, що означення міри
Спочатку зазначимо, що означення міри 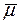 за допомогою рівності (1) коректне, тобто значення
за допомогою рівності (1) коректне, тобто значення 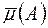 не залежить від запису множин
не залежить від запису множин 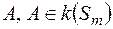 , у вигляді (2). Окрім того із самої рівності (1) випливає, що функція
, у вигляді (2). Окрім того із самої рівності (1) випливає, що функція 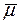 невід’ємна і скінченно-аддитивна на
невід’ємна і скінченно-аддитивна на 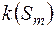 . Покажемо, що функція
. Покажемо, що функція 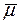 є зчисленно-аддитивна. Нехай
є зчисленно-аддитивна. Нехай 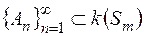 , причому
, причому 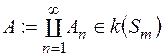 . Множини
. Множини 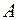 та
та 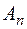 можна записати у вигляді
можна записати у вигляді
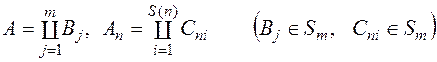 .
.
Оскільки функція 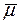 скінченно-аддитивна, то
скінченно-аддитивна, то
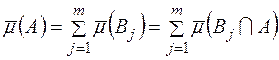 ,
,
внаслідок того, що 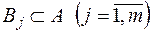 . Тому
. Тому
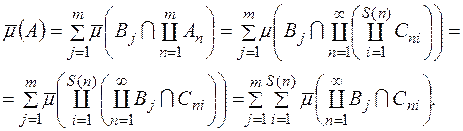
Очевидно, 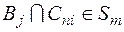 і
і 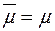 на
на 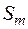 . Оскільки міра
. Оскільки міра 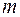 на
на 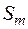 є
є 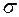 -аддитивна функція, то
-аддитивна функція, то 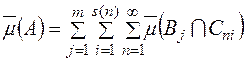 . Тому
. Тому
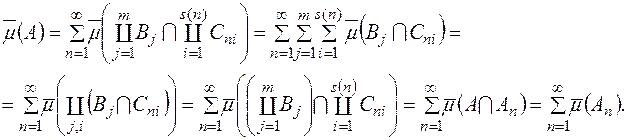 Отже,
Отже, 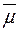 -зчисленно-аддитивна міра, що визначена на
-зчисленно-аддитивна міра, що визначена на 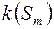 . Єдиність продовження міри
. Єдиність продовження міри 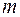 із
із 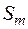 на
на 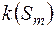 доводиться методом від протилежного.
доводиться методом від протилежного. 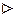
Зауважимо, що перше твердження попередньої теореми справедливе і для скінченно-аддитивної міри 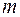 на півкільці
на півкільці 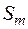 (тоді
(тоді 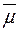 є також скінченно-аддитивна міра на
є також скінченно-аддитивна міра на 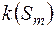 ).
).
Подальше продовження міри 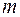 (на ширший ніж
(на ширший ніж 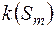 клас множин) можна здійснити за допомогою поняття зовнішньої міри.
клас множин) можна здійснити за допомогою поняття зовнішньої міри.
Якщо 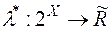 є довільна зовнішня міра, то як випливає з теореми Каратеодорі, клас
є довільна зовнішня міра, то як випливає з теореми Каратеодорі, клас 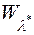 усіх
усіх 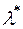 -вимірних множин є
-вимірних множин є 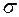 -алгебра множин із одиницею
-алгебра множин із одиницею 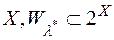 . Однак, ця
. Однак, ця 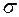 -алгебра може виявитися порівняно вузькою – можливо, що
-алгебра може виявитися порівняно вузькою – можливо, що 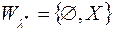 , оскільки ця обставина залежить від
, оскільки ця обставина залежить від 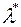 . Виявляється, що у випадку, коли
. Виявляється, що у випадку, коли 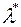 є зовнішня міра, яка породжена мірою
є зовнішня міра, яка породжена мірою 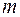 , визначеною на півкільці
, визначеною на півкільці 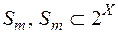 , то
, то 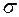 -алгебра
-алгебра 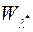 є достатньо широкий клас множин, який включає
є достатньо широкий клас множин, який включає 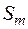 та
та 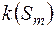 . При цьому справедливе наступне твердження.
. При цьому справедливе наступне твердження.
Теорема2.Якщо 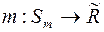 є міра на півкільці
є міра на півкільці 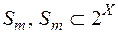 , і
, і 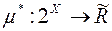 є зовнішня міра, що породжена мірою
є зовнішня міра, що породжена мірою 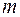 і
і 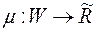 є міра, яка породжена зовнішньою мірою
є міра, яка породжена зовнішньою мірою 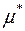 , то міра
, то міра 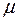 є продовження міри
є продовження міри 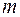 із півкільця
із півкільця 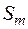 на
на 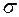 -алгебру
-алгебру 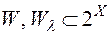 ,
, 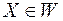 , всіх
, всіх 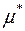 -вимірних множин, тобто
-вимірних множин, тобто 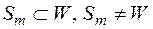 , і
, і 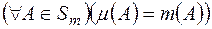 .
.
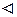 Нам достатньо показати, що
Нам достатньо показати, що 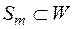 ,оскільки тоді рівність
,оскільки тоді рівність 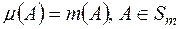 , буде випливати зі співвідношень
, буде випливати зі співвідношень 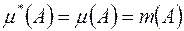 . Оскільки міру
. Оскільки міру 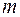 можна єдиним способом продовжити з півкільця
можна єдиним способом продовжити з півкільця 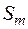 на кільце
на кільце 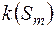 , то в формулюванні теореми можна вважати, що
, то в формулюванні теореми можна вважати, що 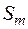 - кільце множин.
- кільце множин.
Нехай 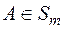 . Зафіксуємо число
. Зафіксуємо число 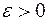 . Візьмемо довільну множину
. Візьмемо довільну множину 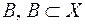 , таку, що
, таку, що 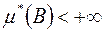 . З означення зовнішньої міри
. З означення зовнішньої міри 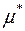 , породженої мірою
, породженої мірою 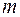 визначеною на півкільці
визначеною на півкільці 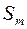 , випливає, що існує така послідовність
, випливає, що існує така послідовність 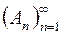 множин
множин 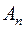 із
із 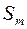 , що
, що 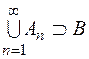 і
і 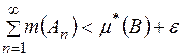 . Враховуючи знову означення зовнішньої міри, породженої мірою на півкільці (у нас на кільці) та скінчену аддитивність міри
. Враховуючи знову означення зовнішньої міри, породженої мірою на півкільці (у нас на кільці) та скінчену аддитивність міри 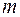 на
на 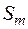 , дістаємо
, дістаємо
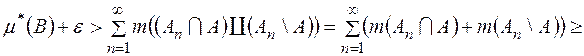
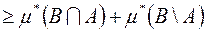 .
.
Переходячи тут до границі при 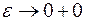 , дістанемо
, дістанемо
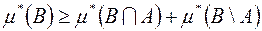
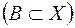 .
.
Остання нерівність справедлива і коли 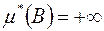 .
.
Оскільки справедлива нерівність, що протилежна до попередньої нерівності, то 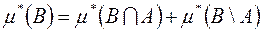
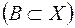 .
.
Отже, множина 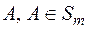 , є
, є 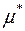 -вимірна, тобто
-вимірна, тобто 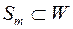 . Зрозуміло, що
. Зрозуміло, що 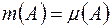 .
.
Означення. Міра 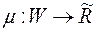 із попередньої теореми називається стандартним продовженням (продовженням за Каратеодорі) міри
із попередньої теореми називається стандартним продовженням (продовженням за Каратеодорі) міри 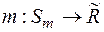 із півкільця
із півкільця 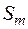 на
на 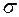 -алгебру
-алгебру 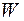 , а
, а 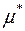 -вимірні множини при цьому називається
-вимірні множини при цьому називається 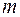 -вимірними.
-вимірними.
Якщо 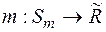 є довільна міра на півкільці
є довільна міра на півкільці 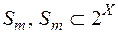 ,
, 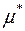 -зовнішня міра, що породжена мірою
-зовнішня міра, що породжена мірою 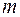 , то, як можна показати
, то, як можна показати
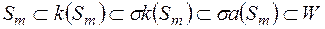 ,
,
де 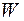 –
– 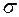 -алгебра всіх
-алгебра всіх 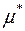 -вимірних (
-вимірних ( 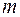 – вимірних) множин.
– вимірних) множин.
Як випливає із попереднього, стандартне продовження 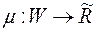 довільної міри
довільної міри 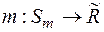 із півкільця
із півкільця 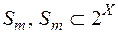 , на
, на 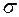 -алгебру
-алгебру 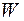 ,
, 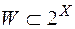 , є повна міра.
, є повна міра.
Можна показати, що продовження 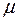 довільної
довільної 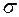 -скінченної міри
-скінченної міри 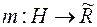 із кільця
із кільця 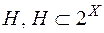 , на
, на 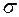 - кільце
- кільце 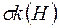 єдине і
єдине і 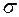 -скінчене.
-скінчене.
Якщо 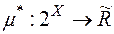 є зовнішня міра, що породжена мірою
є зовнішня міра, що породжена мірою 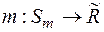 , яка визначена на півкільці
, яка визначена на півкільці 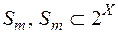 , і
, і 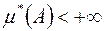 , то, як можна показати,
, то, як можна показати, 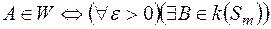
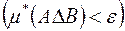 , де
, де 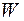 –
– 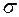 -алгебра усіх
-алгебра усіх 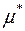 -вимірних множин. Іншими словами, при вказаних умовах множина
-вимірних множин. Іншими словами, при вказаних умовах множина 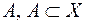 , є
, є 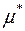 -вимірна тоді і лише тоді, коли її з будь-якою точністю
-вимірна тоді і лише тоді, коли її з будь-якою точністю 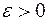 можна “наблизити” множинами із
можна “наблизити” множинами із 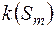 . Сукупність
. Сукупність 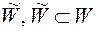 , усіх
, усіх 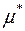 -вимірних множинах
-вимірних множинах 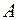 таких, що
таких, що 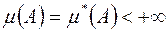 , утворює
, утворює 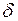 -кільце. Множина
-кільце. Множина 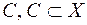 ,
, 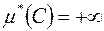 , є
, є 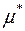 -вимірна тоді і лише тоді, коли
-вимірна тоді і лише тоді, коли 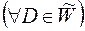
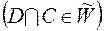 . Якщо міра
. Якщо міра 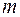 , окрім того,
, окрім того, 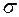 –скінченна, то
–скінченна, то 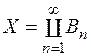 , де
, де 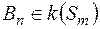 (
( 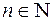 ). В цьому випадку, як можна показати, множина
). В цьому випадку, як можна показати, множина 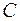 ,
, 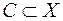 ,
, 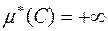 є
є 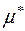 –вимірна тоді і лише тоді, коли (
–вимірна тоді і лише тоді, коли ( 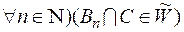 , причому
, причому 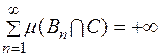 .
.
Дата добавления: 2015-07-24; просмотров: 944;
