Міра Лебега-Стільтьєса на прямій.

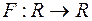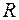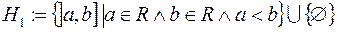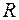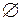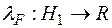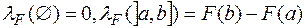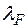Нехай дано функцію , яка неспадна і неперервна справа на . На півкільці всіх піввідкритих проміжків із разом із множиною розглянемо функцію , що задається з допомогою співвідношень: , коли . Можна переконатися у тому, що функція є міра на півкільці 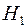. Цю міру, згідно із відомою теоремою, єдиним способом можна продовжити до міри, визначеної на кільці 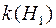. Останню міру також позначимо через 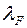, 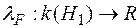. Далі позначимо через 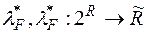, зовнішню міру, що породжена мірою 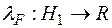, а через 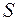-клас усіх 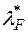‑вимірних підмножин множини 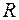. Згідно із відомими теоремами, що доводилися в загальному випадку, клас є сігма­–алгебра множин а функція 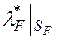, яку ми позначимо через 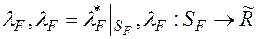, є міра, причому ця міра є продовженням міри 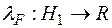із півкільця 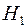, на ­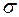–алгебру .

Означення. Множини із 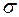-алгебри називаються множинами вимірними в розумінні Лебега-Стільтьєса, а функція 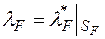називається мірою Лебега-Стільтьєса .

Можна показати, що 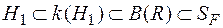. Звідси зокрема випливає, що всі борелеві множини із 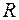є вимірні в розумінні Лебега-Стільтьєса.

Очевидно, звичайна міра Лебега 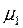на прямій 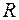є той частковий випадок міри Лебега-Стільтьєса, коли 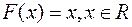. Якщо розглянути довільний сегмент 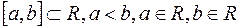, то сукупність усіх вимірних в розумінні Лебега-Стільтьєса множин, що включаються в 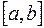, утворює також 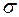-алгебру із одиницею 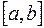, а звуження 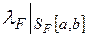функції 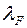із на є також міра. Цю міру ми також будемо позначати через 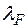і називати мірою Лебега-Стільтьєса.