Поняття вимірної множини.
Виявляється, що міру можна побудувати на основі більш широкого поняття, яким є поняття зовнішньої міри.
Означення 1. Функція 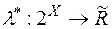 , де
, де 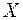 - довільна непорожня множина, називається зовнішньою мірою, якщо виконуються умови:
- довільна непорожня множина, називається зовнішньою мірою, якщо виконуються умови:
1) 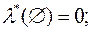
2) 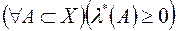 ;
;
3) 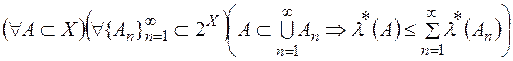 .
.
Зауважимо, що із останньої вимоги випливає 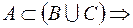
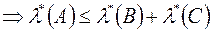 , а також монотонність зовнішньої міри тобто твердження
, а також монотонність зовнішньої міри тобто твердження 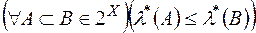 .
.
Часто використовується зовнішня міра, що побудована наступним способом. Якщо 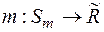 , є міра, що задана на півкільці
, є міра, що задана на півкільці 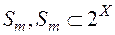 , то розглянемо функцію
, то розглянемо функцію 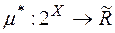 таку, що
таку, що 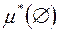 =0,
=0, 
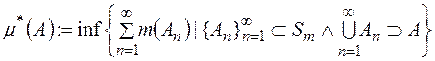 , якщо існує принаймні одне покриття множини
, якщо існує принаймні одне покриття множини 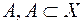 , зчисленною сукупність
, зчисленною сукупність 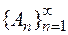 множин
множин 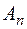 із
із 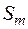 (точна нижня межа відшукується від сукупності сум
(точна нижня межа відшукується від сукупності сум 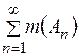 , які відповідають вказаним покриттям множини
, які відповідають вказаним покриттям множини 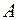 ), і
), і 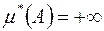 , якщо не існує жодного покриття множини
, якщо не існує жодного покриття множини 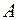 , вказаного вище. Можна показати, що функція
, вказаного вище. Можна показати, що функція 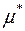 , побудована вказаним способом, є зовнішня міра. Вона називається зовнішньою мірою породженою мірою
, побудована вказаним способом, є зовнішня міра. Вона називається зовнішньою мірою породженою мірою 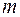 , визначеною на півкільці
, визначеною на півкільці 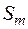 . Ця зовнішня міра, як легко переконатися, володіє властивістю
. Ця зовнішня міра, як легко переконатися, володіє властивістю 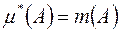 для кожної множини
для кожної множини 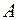 із
із 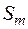 .
.
Повертаючись до загального випадку, розглянемо довільну зовнішню міру 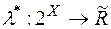 . Оскільки для довільних множин
. Оскільки для довільних множин 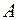 та
та 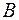 із
із 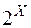 виконується
виконується 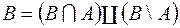 , то
, то
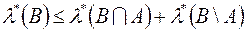 , (1)
, (1)
причому (1) перетворюється в рівність для кожної множини 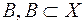 , такої, що
, такої, що 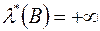 .
.
Важливим є той випадок, коли (1) перетворюється в рівність, справедливу для фіксованої множини 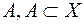 , і довільної множини
, і довільної множини 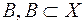 .
.
Означення 2. Множина 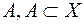 , називається
, називається 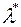 - вимірною (вимірною відносно зовнішньої міри
- вимірною (вимірною відносно зовнішньої міри 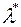 ), якщо
), якщо
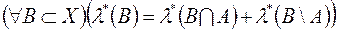 . (2)
. (2)
Зрозуміло, що умова (2) виконується для всіх множин 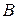 таких, що
таких, що 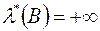 . Отже, множина
. Отже, множина 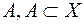 , є
, є 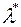 - вимірна тоді і лише тоді, коли (2) виконується для всіх множин
- вимірна тоді і лише тоді, коли (2) виконується для всіх множин 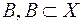 , таких, що
, таких, що 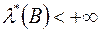 .
.
Позначимо сукупність усіх 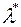 - вимірних підмножин множини
- вимірних підмножин множини 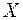 через
через 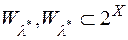 , і розглянемо функцію
, і розглянемо функцію 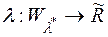 , яка є звуженням функції
, яка є звуженням функції 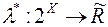 із
із 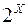 на клас
на клас 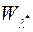 тобто таку функцію, що
тобто таку функцію, що 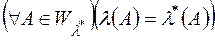 або інакше
або інакше 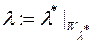 .
.
Теорема Каратеодорі.Якщо 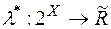 є довільна зовнішня міра, то сукупність
є довільна зовнішня міра, то сукупність 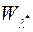 усіх
усіх 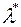 - вимірних множин є
- вимірних множин є 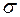 -алгебра множин із одиницею
-алгебра множин із одиницею 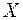 , а функція
, а функція 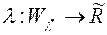 , яка є звуженням функції
, яка є звуженням функції 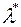 із
із 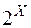 на клас
на клас 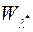 , є міра.
, є міра.
 Оскільки
Оскільки 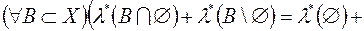
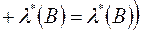 , то
, то 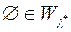 . Якщо
. Якщо 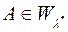 , то множина
, то множина 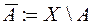 також належить
також належить 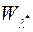 . Справді,
. Справді, 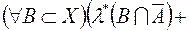
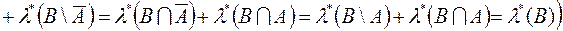 , внаслідок
, внаслідок 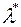 - вимірності множина
- вимірності множина 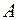 . Очевидно,
. Очевидно, 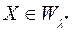 . Це тому, що
. Це тому, що 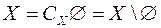 і множина
і множина 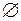 є
є 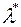 -вимірна.
-вимірна.
Покажемо, що 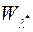 є алгебра множин. Нехай
є алгебра множин. Нехай 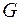 та
та 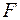 - довільні множини із класу
- довільні множини із класу 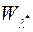 . Тоді при довільній множині
. Тоді при довільній множині 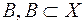 , справедливі рівності
, справедливі рівності 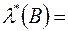 (внаслідок вимірності
(внаслідок вимірності 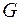 )
) 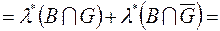 (внаслідок вимірності
(внаслідок вимірності 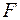 )
) 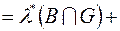
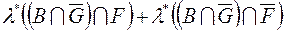 , (3)
, (3)
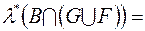 (внаслідок вимірності G)
(внаслідок вимірності G) 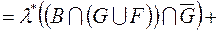
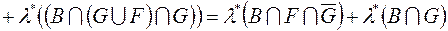 (4)
(4)
Із (3) та (4) випливає, що при довільній множині 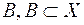 виконується
виконується
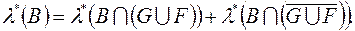 Отже,
Отже, 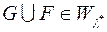 . Окрім того
. Окрім того 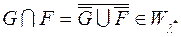 і
і 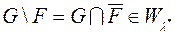 . Отже,
. Отже, 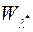 є алгебра із одиницею
є алгебра із одиницею 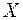 .
.
Покажемо, що 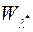 є
є 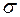 -алгебра множин. Нехай
-алгебра множин. Нехай 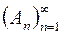 - довільна послідовність множин
- довільна послідовність множин 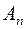 із
із 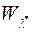 . Покажемо, що
. Покажемо, що 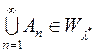 . Оскільки
. Оскільки 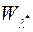 є алгебра множин, то можна вважати, що множини
є алгебра множин, то можна вважати, що множини 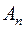 попарно не перетинаються. Тоді для довільної множини
попарно не перетинаються. Тоді для довільної множини 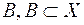 , виконується
, виконується 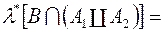 (внаслідок
(внаслідок 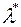 - вимірності
- вимірності 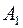 ) =
) = 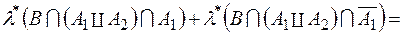
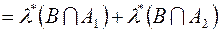 , (5)
, (5)
де 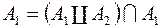 ,
, 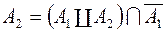 . Із рівності (5) і
. Із рівності (5) і 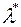 - вимірності множини
- вимірності множини 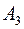 випливає, що при довільній множині
випливає, що при довільній множині  , виконується
, виконується 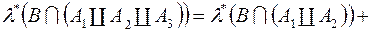
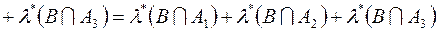 . Методом математичної індукції показуємо, що
. Методом математичної індукції показуємо, що
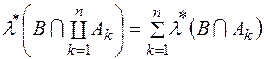 (6)
(6)
при довільному 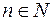 і довільній множині
і довільній множині 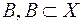 .
.
Враховуючи 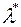 - вимірність множини
- вимірність множини 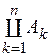 , рівність (6) та монотонність зовнішньої міри, дістанемо, що для довільної множини
, рівність (6) та монотонність зовнішньої міри, дістанемо, що для довільної множини 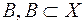 , виконується
, виконується 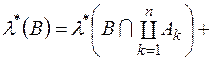
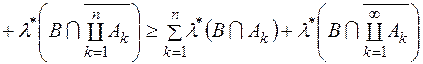 .
.
Переходячи тут до границі при 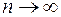 , дістанемо
, дістанемо
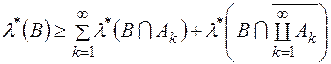 . (7)
. (7)
Оскільки 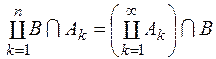 і
і 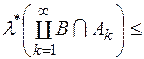
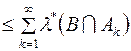 , то дістанемо
, то дістанемо 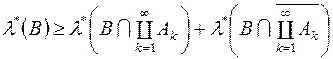 . Оскільки
. Оскільки 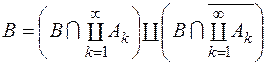 , то
, то 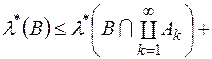
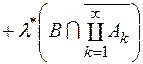 . Отже, для довільної множини
. Отже, для довільної множини 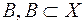 , справедливе
, справедливе 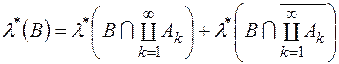 .
.
Тому 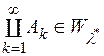 і, отже,
і, отже, 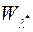 є
є 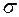 -алгебра множин.
-алгебра множин.
Покажемо 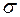 -аддитивність функції
-аддитивність функції 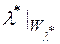 . Якщо в (7) покласти
. Якщо в (7) покласти 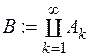 , де
, де 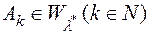 , то дістанемо
, то дістанемо 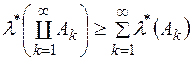 .
.
Оскільки справедлива і протилежна нерівність, то 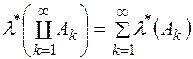 .
.
Отже, 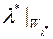 є міра на
є міра на 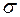 -алгебрі
-алгебрі 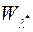 . Теорему доведено.
. Теорему доведено. 
Зауважимо, що міра 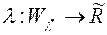 , про яку іде мова в доведеній теоремі, називається мірою, породженою зовнішньою мірою
, про яку іде мова в доведеній теоремі, називається мірою, породженою зовнішньою мірою 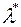 .
.
Ця міра і 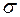 -алгебра
-алгебра 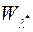 володіють властивостями:
володіють властивостями:
1) 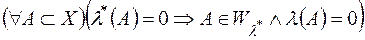 ;
;
2) 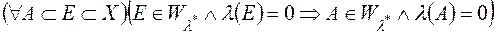 ;
;
3) 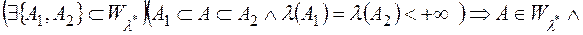
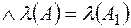 ;
;
4) 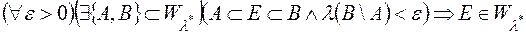 .
.
Зауважимо, що останнє твердження вказує достатню умову 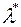 - вимірності множини
- вимірності множини 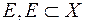 . Можна показати, що
. Можна показати, що
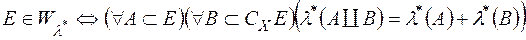 .
.
Означення 3. Міра 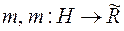 , що визначена на півкільці
, що визначена на півкільці 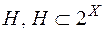 , називається повною, якщо
, називається повною, якщо 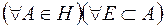
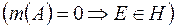 .
.
Із твердження 2) випливає, що міра 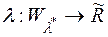 , яка породжена довільною зовнішньою мірою
, яка породжена довільною зовнішньою мірою 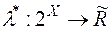 є повна міра на
є повна міра на 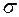 -алгебрі
-алгебрі 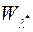 .
.
Дата добавления: 2015-07-24; просмотров: 912;
