Якщо B - -алгебра борелевих множин метричного простору , то B §1.4. Функції, визначені на класах множин. Поняття міри.
Нехай 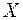 - довільна непорожня множина і
- довільна непорожня множина і  - довільний непорожній клас підмножин множини
- довільний непорожній клас підмножин множини 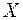 ,
, 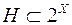 . Позначимо
. Позначимо 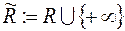 . Будемо розглядати тут функції виду
. Будемо розглядати тут функції виду 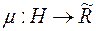 .
.
Означення 1. Функція 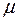 , що визначена на класі множин
, що визначена на класі множин  називається на
називається на  :
:
1) невід'ємною, якщо 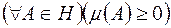 ;
;
2) скінченно-аддитивною, якщо
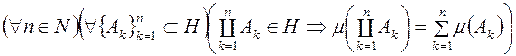 ;
;
3) зчисленно-аддитивною або 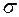 -аддитивною, якщо
-аддитивною, якщо
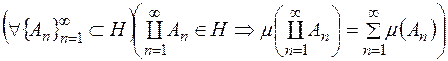
(причому сума ряду може дорівнювати і 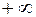 );
);
4) скінченою, якщо 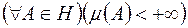 ;
;
5) неспадною, якщо 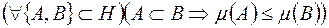 ;
;
6) 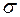 -скінченною, якщо
-скінченною, якщо 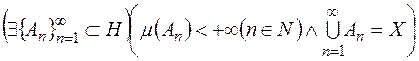 .
.
Очевидно, якщо 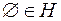 і
і 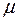 -скінченно-аддитивна функція на
-скінченно-аддитивна функція на  і
і 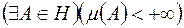 , то
, то 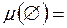 0.
0.
Це випливає зі співвідношень 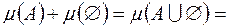
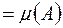 .
.
Окрім того, як можна показати, якщо функція 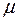 зчисленно-аддитивна на
зчисленно-аддитивна на  , то вона і скінченно-аддитивна на
, то вона і скінченно-аддитивна на  ,але не кожна скінченно-аддитивна функція
,але не кожна скінченно-аддитивна функція 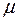 є
є 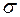 -аддитивна на
-аддитивна на  .
.
Означення 2. Функція 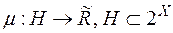 , називається мірою, якщо
, називається мірою, якщо  -півкільце множин і функція
-півкільце множин і функція 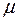 невід’ємна та
невід’ємна та 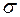 -аддитивна на
-аддитивна на  .
.
Зазначимо, що 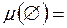 0 для міри
0 для міри 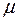 такої, що
такої, що 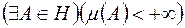 . Скрізь нижче розглядатиметься лише така міра
. Скрізь нижче розглядатиметься лише така міра 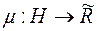 на півкільці
на півкільці  , для якої остання умова виконується.
, для якої остання умова виконується.
Функція 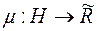 , що визначена на півкільці
, що визначена на півкільці  ,
, 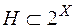 , називається скінченно-аддитивною мірою, якщо вона невід’ємна і скінченно-аддитивна на
, називається скінченно-аддитивною мірою, якщо вона невід’ємна і скінченно-аддитивна на  .
.
Зрозуміло, що міра є скінченно-аддитивна міра, але не кожна скінченно-аддитивна міра є міра.
Ми будемо розглядати тут в основному міру, хоча деякі твердження, які будуть встановлені, справедливі і для скінченно-аддитивної міри.
Означення 3. Міра 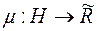 на півкільці
на півкільці  називається
називається 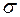 -скінченною (скінченною), якщо функція
-скінченною (скінченною), якщо функція 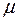 є
є 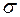 -скінченна (скінченна) на
-скінченна (скінченна) на  .
.
Приклад 1. Якщо 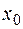 - фіксована точка непорожньої множини
- фіксована точка непорожньої множини 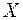 ,
, 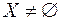 ,
, 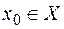 , то функція
, то функція 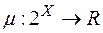 така, що
така, що 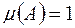 , коли
, коли 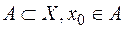 , і
, і 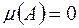 , коли
, коли 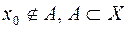 , для кожної множини
, для кожної множини 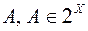 , є міра на
, є міра на 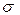 -алгебрі (на кільці)
-алгебрі (на кільці) 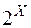 , причому вона скінченна.
, причому вона скінченна.
Приклад 2. Якщо 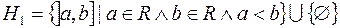 - півкільце всіх найможливіших обмежених півінтервалів в
- півкільце всіх найможливіших обмежених півінтервалів в 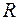 разом з порожньою множиною,
разом з порожньою множиною, 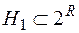 , то функція
, то функція 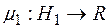 така, що
така, що 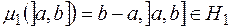 , і
, і 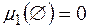 , є міра на
, є міра на 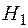 , причому вона скінченна та
, причому вона скінченна та 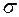 -скінченна.
-скінченна.
Приклад 3. Якщо 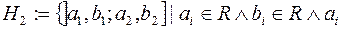
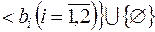 - півкільце усіх найможливіших піввідкритих прямокутників
- півкільце усіх найможливіших піввідкритих прямокутників 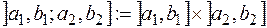 із
із  разом з порожньою множиною,
разом з порожньою множиною, 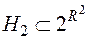 , то функція
, то функція 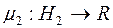 така, що
така, що 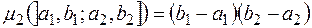 ,
, 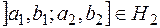 , і
, і 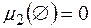 , є скінченна та
, є скінченна та 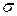 -скінченна міра на
-скінченна міра на 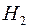 .
.
Основні властивості міри 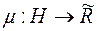 на півкільці
на півкільці 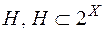 , описуються наступними твердженнями:
, описуються наступними твердженнями:
а) 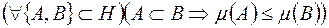 (монотонність міри);
(монотонність міри);
б) 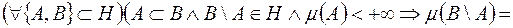
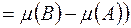 ;
;
в) 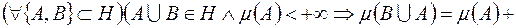
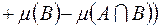 ;
;
г) 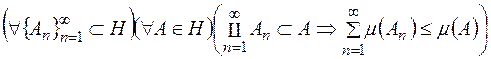 ;
;
д) 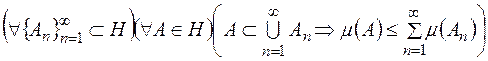 .
.
На основі останньої властивості доводиться, що міра 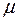 на півкільці
на півкільці  є зчисленно-піваддитивна (
є зчисленно-піваддитивна ( 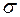 -піваддитивна) функція, тобто
-піваддитивна) функція, тобто
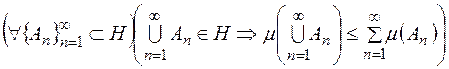 .
.
Зрозуміло, що останнє твердження, а також властивості г), д), справедливі і для довільних скінчених сукупностей множин 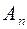 та
та 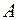 із півкільця
із півкільця  .
.
Дата добавления: 2015-07-24; просмотров: 691;
