Множини метричного простору.
Теорія міри і інтеграла
Міра.
Множини метричного простору.
Нагадаємо тут деякі поняття і факти, які будуть використовуватися пізніше. Через 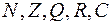 будемо позначати відповідно множину натуральних чисел, кільце цілих чисел, поля раціональних, дійсних та комплексних чисел.
будемо позначати відповідно множину натуральних чисел, кільце цілих чисел, поля раціональних, дійсних та комплексних чисел.
Якщо 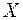 - деяка непорожня множина, то через
- деяка непорожня множина, то через 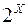 позначимо сукупність всіх підмножин цієї множини,
позначимо сукупність всіх підмножин цієї множини, 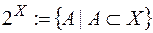 . Очевидно,
. Очевидно, 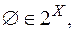
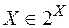 . Відомо, що різниця
. Відомо, що різниця 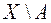 , де
, де 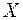 і
і 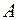 - довільні множини,
- довільні множини, 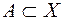 , називається доповненням множини
, називається доповненням множини 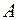 (до множини
(до множини 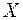 ) і позначається
) і позначається 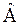 або
або 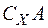 тобто
тобто 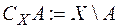 .
.
Для довільної сукупності 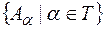 множин
множин 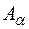 таких, що
таких, що 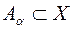 при
при 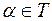 , де
, де 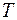 - скінченна або нескінченна множина індексів
- скінченна або нескінченна множина індексів 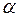 , справедливі рівності
, справедливі рівності
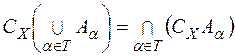 ,
, 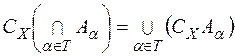 ,
,
які називаються законами двоїстості або законами де Моргана.
Множини 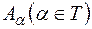 називаються диз’юнктивними, якщо
називаються диз’юнктивними, якщо 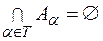 . Об¢єднання таких множин позначається
. Об¢єднання таких множин позначається 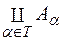 .
.
Відомо, що дві функції 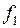 і
і 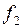 називаються рівними (співпадаючими), якщо
називаються рівними (співпадаючими), якщо 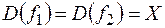 і
і 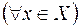
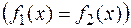 .
.
Якщо 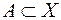 , то функція
, то функція 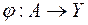 така, що
така, що 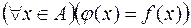 , називається звуженням функції
, називається звуженням функції 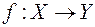 на множину
на множину 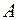 і позначається
і позначається 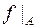 . При цьому функція
. При цьому функція 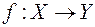 називається продовженням (поширенням) функції
називається продовженням (поширенням) функції 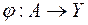 із множини
із множини 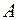 на множину
на множину 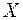 .
.
Нагадаємо, що множина 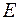 ,
, 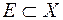 , називається замкнутою в метричному просторі
, називається замкнутою в метричному просторі 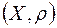 з метрикою
з метрикою 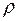 , якщо вона містить всі свої граничні точки. Множина
, якщо вона містить всі свої граничні точки. Множина 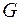 ,
, 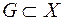 , називається відкритою в метричному просторі
, називається відкритою в метричному просторі 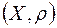 , якщо кожна точка множини
, якщо кожна точка множини 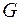 є внутрішньою точкою для неї, тобто належить
є внутрішньою точкою для неї, тобто належить 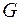 разом зі всіма точками деякого свого околу. Відомо, що множина
разом зі всіма точками деякого свого околу. Відомо, що множина 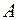 ,
, 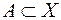 , є відкрита (замкнута) в метричному просторі
, є відкрита (замкнута) в метричному просторі 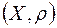 тоді і лише тоді, коли множина
тоді і лише тоді, коли множина 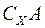 замкнута (відкрита) в
замкнута (відкрита) в 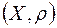 .
.
Очевидно відкрита 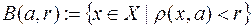 та замкнута,
та замкнута, 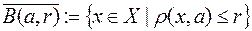 ,
, 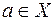 ,
, 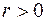 , кулі метричного простору
, кулі метричного простору 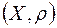 є відповідно відкрита та замкнута множини в
є відповідно відкрита та замкнута множини в 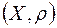 .
.
Справедливі наступні твердження:
1) якщо 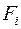 – замкнуті множини і
– замкнуті множини і 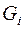 - відкриті множини метричного простору
- відкриті множини метричного простору 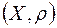 ,
, 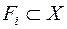 ,
, 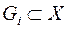
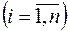 , то при довільному
, то при довільному 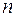 ,
, 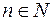 , множина
, множина 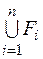 замкнута, а множина
замкнута, а множина 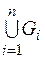 відкрита в
відкрита в 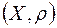 .
.
2) якщо 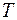 - довільна скінченна або нескінченна множина індексів і множини
- довільна скінченна або нескінченна множина індексів і множини 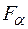 ,
, 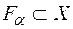 при
при 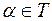 , та
, та 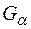 ,
, 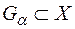 при
при 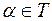 , відповідно замкнуті та відкриті в метричному просторі
, відповідно замкнуті та відкриті в метричному просторі 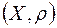 , то множини
, то множини 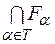 ,
, 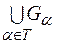 є відповідно замкнута та відкрита в
є відповідно замкнута та відкрита в 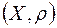 .
.
Можна показати, що кожна непорожня відкрита множина 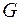 метричного простору
метричного простору 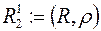 ,
, 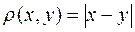
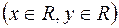 (тобто відкрита множина на числовій прямій) є або вся множина
(тобто відкрита множина на числовій прямій) є або вся множина 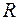 або об¢єднання не більш ніж зчисленної сукупності інтервалів (обмежених або необмежених), які попарно не перетинаються і кінці яких не належать
або об¢єднання не більш ніж зчисленної сукупності інтервалів (обмежених або необмежених), які попарно не перетинаються і кінці яких не належать 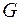 (вони називаються складовими інтервалами множини
(вони називаються складовими інтервалами множини 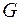 ).
).
Кожна замкнута множина 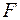 метричного простору
метричного простору 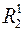 є або вся множина
є або вся множина 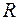 або утворюється шляхом вилучення із
або утворюється шляхом вилучення із 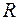 не більш ніж зчисленної сукупності інтервалів, які попарно не перетинаються і кінці яких належать
не більш ніж зчисленної сукупності інтервалів, які попарно не перетинаються і кінці яких належать 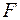 , якщо ці кінці не є символи
, якщо ці кінці не є символи 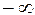 та
та 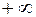 (такі інтервали називаються суміжними інтервалами для
(такі інтервали називаються суміжними інтервалами для 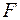 ).
).
Якщо 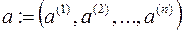 ,
, 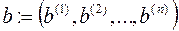 - дві фіксовані точки із
- дві фіксовані точки із 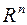 ,
, 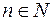 такі, що
такі, що 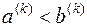
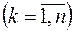 , то множина
, то множина 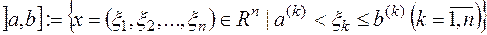 називається півінтервалом в
називається півінтервалом в 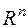 або піввідкритим паралелепіпедом в
або піввідкритим паралелепіпедом в 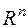 .
.
Можна показати, що кожна непорожня відкрита множина із метричного простору 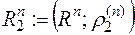 , де
, де 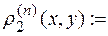
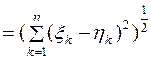 ,
, 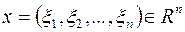 ,
, 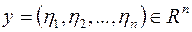
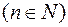 , є або вся множина
, є або вся множина 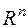 або об¢єднання зчисленної сукупності півінтервалів із
або об¢єднання зчисленної сукупності півінтервалів із 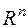 , які попарно не перетинаються. Вказане об¢єднання не може складатися зі скінченної сукупності півінтервалів.
, які попарно не перетинаються. Вказане об¢єднання не може складатися зі скінченної сукупності півінтервалів.
З іншого боку, як можна показати, кожна непорожня відкрита множина із 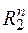 є або вся множина
є або вся множина 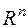 або об¢єднання не більш ніж зчисленної сукупності відкритих куль простору
або об¢єднання не більш ніж зчисленної сукупності відкритих куль простору  .
.
Дата добавления: 2015-07-24; просмотров: 1018;
