Породжені класи множин.
Нехай  - довільний непорожній клас множин,
- довільний непорожній клас множин, 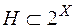 . Можна показати, що існує єдине кільце
. Можна показати, що існує єдине кільце 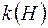 , яке включає клас
, яке включає клас  і яке включається в кожне інше кільце, що включає
і яке включається в кожне інше кільце, що включає  і включається в
і включається в 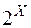 . Таке кільце
. Таке кільце 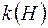 називається мінімальним кільцем над класом
називається мінімальним кільцем над класом  або кільцем, породженим класом
або кільцем, породженим класом  . Кільце
. Кільце 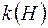 можна означити також за допомогою рівності:
можна означити також за допомогою рівності:
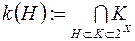 (
( 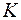 - кільце),
- кільце),
оскільки перетин довільної сукупності кілець 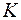 ,
, 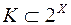 , є кільце.
, є кільце.
Аналогічно можна означити алгебру 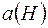 ,
, 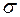 -кільце
-кільце 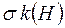 ,
, 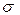 -алгебру
-алгебру 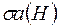 , які породжені класом множин
, які породжені класом множин  (які мінімальні над класом
(які мінімальні над класом  ). Зокрема, це можна зробити наступним способом:
). Зокрема, це можна зробити наступним способом:
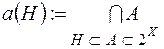 ,
, 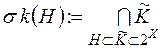 ,
, 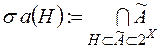 ,
,
де 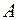 ,
, 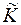 ,
, 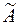 є відповідно довільні алгебра,
є відповідно довільні алгебра, 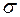 -кільце та
-кільце та 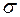 -алгебра, що включають
-алгебра, що включають  і включаються в
і включаються в 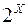 .
.
Якщо 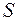 - довільне півкільце,
- довільне півкільце, 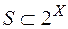 , то кільце
, то кільце 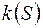 , що породжене півкільцем
, що породжене півкільцем 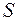 , є сукупність усіх найможливіших множин
, є сукупність усіх найможливіших множин 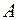 ,
, 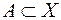 , які можна записати у вигляді
, які можна записати у вигляді 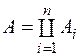 ,
, 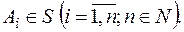 Наприклад, кільце
Наприклад, кільце 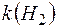 , що породжене півкільцем
, що породжене півкільцем 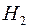 усіх піввідкритих прямокутників із
усіх піввідкритих прямокутників із  , є сукупність усіх найможливіших елементарних множин із
, є сукупність усіх найможливіших елементарних множин із  , тобто множин, які являють собою скінченні об’єднання піввідкритих прямокутників із
, тобто множин, які являють собою скінченні об’єднання піввідкритих прямокутників із  , які попарно не перетинаються (разом з множиною
, які попарно не перетинаються (разом з множиною 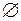 ).
).
Якщо 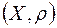 - довільний метричний простір і
- довільний метричний простір і 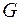 - клас усіх відкритих множин цього простору,
- клас усіх відкритих множин цього простору, 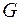
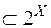 , то мінімальна
, то мінімальна 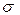 -алгебра
-алгебра 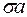 (G) над класом G називається
(G) над класом G називається 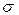 -алгеброю борелевих множин цього метричного простору і позначається B
-алгеброю борелевих множин цього метричного простору і позначається B 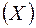 , B
, B 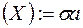 ( G).
( G).
Можна довести наступні твердження:
1) Якщо 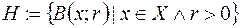 , де
, де 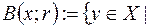
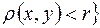 - відкрита куля метричного простору
- відкрита куля метричного простору 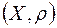 , то B
, то B 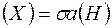 ;
;
2) Якщо F - клас усіх замкнутих множин метричного простору 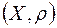 , то B
, то B 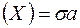 (F)
(F) 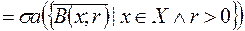 , де
, де 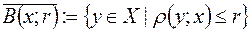 - замкнута куля цього простору;
- замкнута куля цього простору;
3) Кожна одноелементна та кожна зчисленна множини точок метричного простору 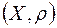 є борелеві множини;
є борелеві множини;
4) Множини 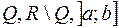
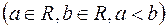 точок метричного простору
точок метричного простору 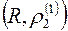 зі стандартною метрикою
зі стандартною метрикою 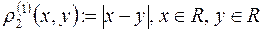 , заданою на
, заданою на 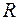 , є борелеві множини (належать B
, є борелеві множини (належать B 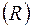 );
);
Дата добавления: 2015-07-24; просмотров: 699;
