Зчисленні множини

Множина називається зчисленною, якщо вона рівнопотужна множині натуральних чисел N. Множина зчисленна, якщо існує хоча б одна бієкція цієї множини в множину N. Іншими словами, множина зчисленна, якщо її елементи можна пронумерувати натуральними числами і номери не будуть повторюватися.

Раніше ми з’ясували, що множина парних натуральних чисел N₂ є зчисленною.

Задамо відображення f : Z → N так: f(z)=2z при z>0, f(z)=2|z|+1 при z≤0. Воно бієктивне і, значить, множина цілих чисел Z також є зчисленною.

Покажемо, що множина N ´ N рівнопотужна множині N. Дійсно, з наведеної далі схеми

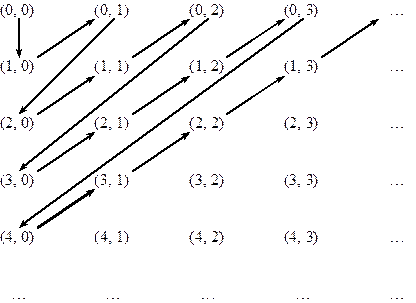
бачимо, що відображення 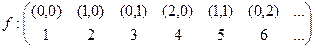, тобто f : N ´ N → N є бієкцією.

Інший варіант бієктивного відображення f : N ´ N → Nнаведено далі.

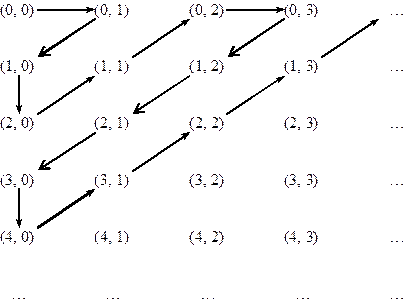
Покажемо, що множина Z ´ Z рівнопотужна множині N. Далі наведено схему, яка задає відповідне бієктивне відображення f :Z ´ Z → N

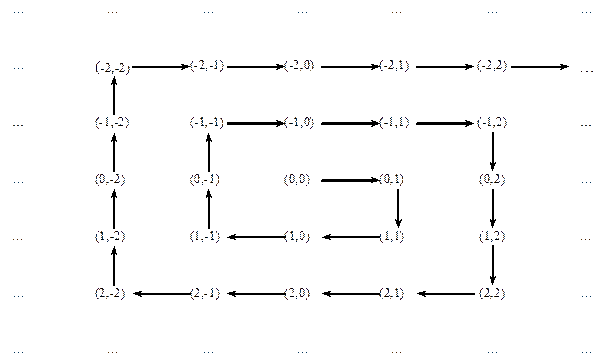
Таким чином, множина Z ´ Z також є зчисленною.

Покажемо, що й множина раціональних чисел зчисленна. Множину раціональних чисел можна розглядати так: Q = {(m,n) | m − ціле число, n − натуральне число, найбільший спільний дільник m та n дорівнює 1}.

На наведеній далі схемі зображено впорядковані пари - елементи множини Q₁ = {(m,n) | m − ціле число, n − натуральне число}. Оскільки різні такі пари можуть задавати одне і те ж раціональне число (наприклад, пари (1,2), (2,4), (3,6) і т.д. задають число ½), то кожен елемент множини Q на схемі зображаємо променем, початком якого є пара (m,n), у цьому разі найбільший спільний дільник m та n дорівнює 1. Починаючи з неї і через всі подальші пари, що задають те саме раціональне число, проводимо промінь – по суті об’єднуємо такі пари в одну групу.

Нумеруємо елементи множини Q прямими зі стрілками, що послідовно з’єднують початки променів. Загальний шлях нумерації складається з низки умовних півкіл. У кожному півколі прямі зі стрілками з’єднують ті пари, що мають рівні суми |m| + |n|.

Усі розглянуті досі множини виявилися зчисленними множинами. Виникає запитання: а чи існують нескінченні множини, які не є зчисленними ? Відповідь отримаємо далі.