Потужність континууму

Теорема 2 (Кантора) . Множина дійсних чисел з інтервалу (0, 1) не є зчисленною.

Дійсно, доведемо, що множина X = (0, 1) дійсних чисел, які задовольняють нерівність 0 ≤ x ≤ 1, не є зчисленною.

Доведення проведемо від протилежного. Припустимо, що X зчисленна й існує деяка бієкція N на Х, тобто елементи X можуть бути записані y вигляді деякої послідовності x₁, x₂, x₃, …, елементи якої попарно різні. Крім того, розглянемо дійсне число ξ, яке визначимо так: перед комою поставимо 0, потім як j-й десятковий знак виберемо довільне ціле число між 1 і 8, яке відрізняється від j-го десяткового знака числа х_j. Таким способом ми утворюємо нескінченний дріб, що визначає деяке число ξ. Для довільного натурального j маємо таке. Оскільки j-й десятковий знак числа ξ відрізняється від j-го десяткового знака числа х_j і всі десяткові знаки числа ξ відрізняються від 0 і 9, то ξ ≠ х_j (не допускаємо знаків 0 і 9, бо 0,102000... і 0,101999... одне і те ж саме число). Значить число ξ не збігається ні з одним з чисел послідовності x₁, x₂, x₃, … Ми отримали суперечність. Це й доводить теорему.

Будемо потужність множини X = (0, 1) називати потужністю континууму. Потужність континууму - це також потужність множини всіх дійсних чисел, оскільки 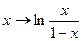є бієкцією (0, 1) на R.

Дійсно, нехай x1≠x2 Припустимо, що 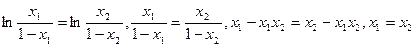суперечність Отже, це відображення ін’єктивне.

Це відображення також є сюр’єктивним, бо з рівності .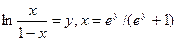

Наведемо без доведення теорему.

Теорема 3 (Бернштейна). Нехай X та Y – дві довільні множини. Тоді 1) або існує ін’єкція X в Y, або існує ін’єкція Y в X (обидві обставини не виключають одна одну); 2) якщо існує одночасно ін’єкція X в Y та ін’єкція Y в X, то існує також бієкція X на Y.

Наслідок. Для заданих множин X та Y є тільки три можливості:

а) існує ін’єкція X в Y і не існує ін’єкція Y в X. В цьому випадку говорять, що Y має потужність строго більшу потужності X, або що X має потужність, строго меншу потужності Y;

б) існує ін’єкція Y в X і не існує ін’єкція X в Y. Тоді X має потужність строго більшу потужності Y або Y має потужність, строго меншу потужності X;

в) існує бієкція X в Y. У цьому випадку кажуть, що X і Y мають однакову потужність або рівнопотужні.

Теорема 4. Якою б не була множина X, множина її підмножин має потужність, строго більшу потужності X.

Виходячи з останньої теореми, для нескінченних множин існує нескінченне число класів рівнопотужних множин.

На завершення сформулюємо континуум-гіпотезу. Згідно цієї гіпотези, клас множини P(N) іде одразу за класом множини N(тобто між ними не можна вставити проміжний клас). Узагальнена континуум-гіпотеза полягає в припущенні, що при довільній множині X клас множини P(X) іде безпосередньо за класом множини X. Доведено (П. Коен, 1968 р.), що континуум-гіпотеза не має рішення – її не можливо ані довести, ані спростувати, можна тільки прийняти її або протилежне їй твердження як аксіому.