Векторні послідовності. Поняття границі векторної послідовності

Нехай будь-якому 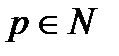ставиться в співвідношення деяка точка (чи вектор) 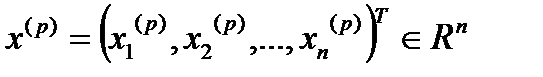. Тоді кажуть, що в просторі 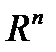визначена векторна послідовність .

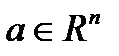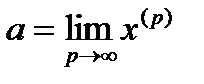Визначення 5. Точка називається границею векторної послідовності і позначається: , якщо

для 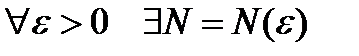, що для 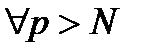виконується: .

Геометричний зміст: Точка 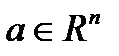є границею векторної послідовності , якщо будь-який окіл точки 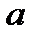в просторі 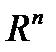містить нескінченно багато елементів послідовності, а поза околом їх може бути лише скінченна кількість.

Приклад. Нехай подана векторна послідовність , для якої 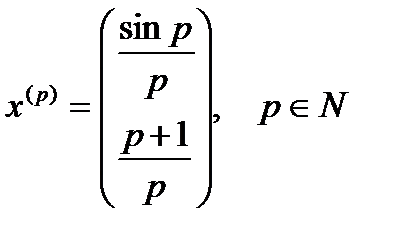. Довести, що .

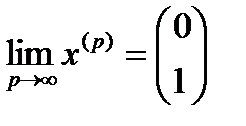За визначенням 5 треба показати, що

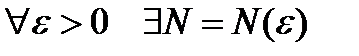, що для : .

.

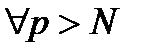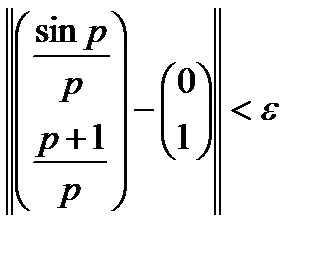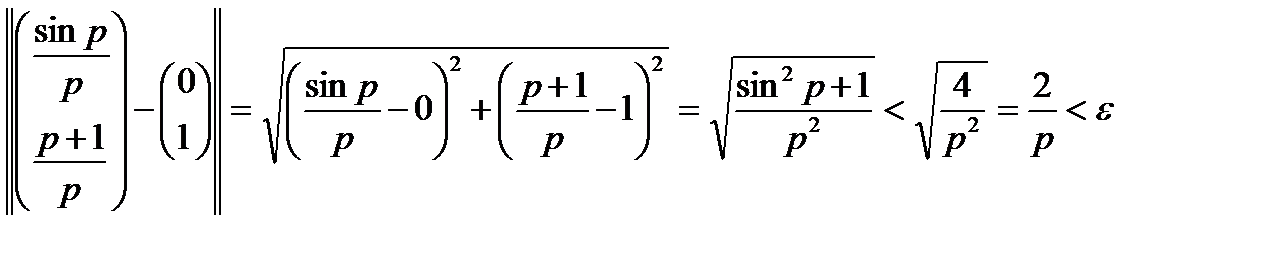Якщ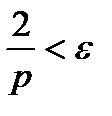о , то :

.

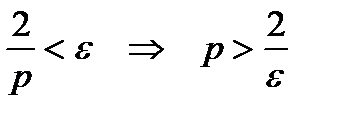Таким чином, нерівність виконується для нескінченної кількості елементів послідовності, номери яких 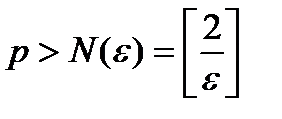, що й потрібно було довести.