Міра Лебега в .
Можна показати, що клас 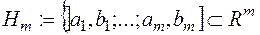
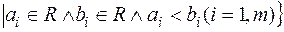
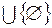 усіх піввідкритих паралелепіпедів
усіх піввідкритих паралелепіпедів 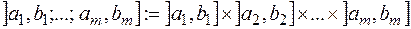 простору
простору 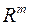 разом з порожньою множиною утворює півкільце множин без одиниці. Зокрема
разом з порожньою множиною утворює півкільце множин без одиниці. Зокрема 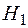 та
та 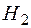 є, відповідно, півкільце усіх півінтервалів
є, відповідно, півкільце усіх півінтервалів 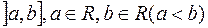 в
в 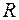 та усіх піввідкритих прямокутників
та усіх піввідкритих прямокутників 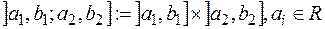 ,
, 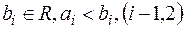 в
в 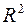 разом із
разом із 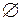 . Можна переконатися в тому, що функція
. Можна переконатися в тому, що функція 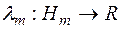 така, що
така, що 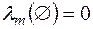 і
і 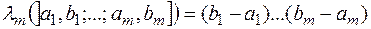 ,
, 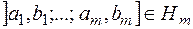 , є
, є 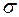 -скінченна міра на півкільці
-скінченна міра на півкільці 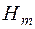 . Цю міру, внаслідок відомої теореми, можна єдиним способом продовжити до міри
. Цю міру, внаслідок відомої теореми, можна єдиним способом продовжити до міри 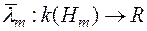 , визначеної на кільці
, визначеної на кільці 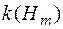 , причому
, причому 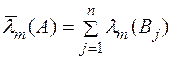 для кожної множини
для кожної множини 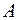 із
із 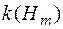 , якщо
, якщо 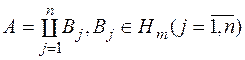 . Якщо
. Якщо  є зовнішня міра, що породжена мірою
є зовнішня міра, що породжена мірою 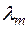 , то в результаті стандартного продовження міри
, то в результаті стандартного продовження міри 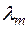 , як це випливає із теореми, що справедливі в загальному випадку, клас
, як це випливає із теореми, що справедливі в загальному випадку, клас 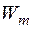 усіх
усіх 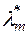 –вимірних множин із
–вимірних множин із 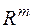 являє собою
являє собою 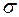 -алгебру множин із одиницею
-алгебру множин із одиницею 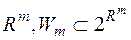 , а функція
, а функція 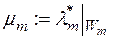 є міра на
є міра на 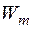 .
.
Означення. Множини із 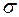 –алгебри
–алгебри 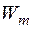 називаються множинами вимірними за Лебегом, а функція
називаються множинами вимірними за Лебегом, а функція 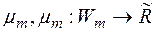 , така, що
, така, що 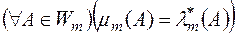 , називається мірою Лебега в
, називається мірою Лебега в 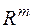 або продовженням міри
або продовженням міри 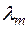 із півкільця
із півкільця 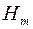 на
на 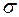 -алгебру
-алгебру 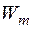 за Лебегом.
за Лебегом.
Зрозуміло, що можна розглядати одномірну (лінійну), двомірну (плоску) міри Лебега і т.д. Всі факти, які раніше були відмічені для міри, породженої зовнішньою мірою, яка породжена довільною мірою, визначеною на півкільці, справедливі зокрема і для міри Лебега в 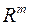 .Із вказаних загальних тверджень випливає, що
.Із вказаних загальних тверджень випливає, що 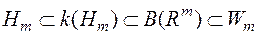 .
.
Отже, всі борелеві множини із 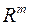 є вимірні за Лебегом. Зокрема вимірні за Лебегом всі відкриті та замкнуті множини із
є вимірні за Лебегом. Зокрема вимірні за Лебегом всі відкриті та замкнуті множини із 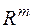 і їх скінченні або зчисленні об’єднання та перетини, всі найможливіші паралелепіпеди (відкриті, замкнуті, піввідкриті, обмежені і необмежені і т.д). При цьому значення лебегової міри обмеженого паралелепіпеда дорівнює добутку усіх його вимірів. Кожна скінченна та кожна зчисленна множини точок із
і їх скінченні або зчисленні об’єднання та перетини, всі найможливіші паралелепіпеди (відкриті, замкнуті, піввідкриті, обмежені і необмежені і т.д). При цьому значення лебегової міри обмеженого паралелепіпеда дорівнює добутку усіх його вимірів. Кожна скінченна та кожна зчисленна множини точок із 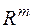 вимірні за Лебегом і значення їх лебегової міри дорівнює 0. Звичайно, що існують вимірні за Лебегом множини із
вимірні за Лебегом і значення їх лебегової міри дорівнює 0. Звичайно, що існують вимірні за Лебегом множини із 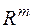 , що не є борелевими множинами.
, що не є борелевими множинами.
Значення Лебегової міри кожної відкритої непорожньої множини із 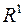 дорівнює сумі (скінченій або нескінченній) довжин усіх її складових інтервалів.
дорівнює сумі (скінченій або нескінченній) довжин усіх її складових інтервалів.
Як впливає із загальних положень, достатньою умовою вимірності множини 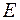 ,
, 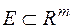 , за Лебегом є вимога
, за Лебегом є вимога 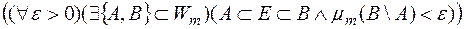 .
.
Як можна показати, вказана вище множина 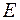 є вимірна за Лебегом тоді і лише тоді, коли
є вимірна за Лебегом тоді і лише тоді, коли 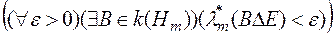 .
.
Сігма-алгебра 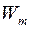 є достатньо широкий клас множин, як це впливає із попереднього, але при кожному
є достатньо широкий клас множин, як це впливає із попереднього, але при кожному 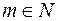 в просторі
в просторі 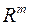 існують (навіть обмежені) множини, що не є вимірними за Лебегом. В
існують (навіть обмежені) множини, що не є вимірними за Лебегом. В 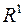 такі множини можна побудувати наступним способом. Всі точки довільної вимірної за Лебегом множини
такі множини можна побудувати наступним способом. Всі точки довільної вимірної за Лебегом множини 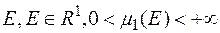 , розіб’ємо на класи, що попарно не перетинаються, віднісши дві точки
, розіб’ємо на класи, що попарно не перетинаються, віднісши дві точки  та
та 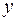 із
із 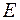 до одного класу тоді і лише тоді коли
до одного класу тоді і лише тоді коли 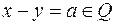 .Це можна зробити наступним способом: кожній точці
.Це можна зробити наступним способом: кожній точці  із
із 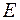 поставимо у відповідність клас
поставимо у відповідність клас 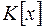 , що складається із усіх таких точок множини
, що складається із усіх таких точок множини 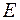 , які мають вигляд
, які мають вигляд 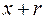 , де
, де 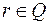 ; зокрема
; зокрема 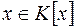 . Можна показати, що будь-які два класи
. Можна показати, що будь-які два класи 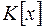 та
та 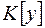 ,
, 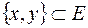 , або повністю співпадають (тоді ми їх не будемо розрізняти) або не перетинаються. Вибравши довільним чином із кожного такого класу по одній точці, дістанемо множину
, або повністю співпадають (тоді ми їх не будемо розрізняти) або не перетинаються. Вибравши довільним чином із кожного такого класу по одній точці, дістанемо множину 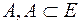 , яка, як можна показати, не є вимірна за Лебегом. Отже, кожна вимірна за Лебегом множина
, яка, як можна показати, не є вимірна за Лебегом. Отже, кожна вимірна за Лебегом множина 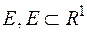 , така, що
, така, що 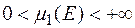 , включає підмножину, яка не є вимірною за Лебегом.
, включає підмножину, яка не є вимірною за Лебегом.
Зауваження. Зазначимо, що деякі автори терміни продовження міри за Лебегом, вимірність множини за Лебегом, міра Лебега використовують не лише при розгляді цих понять в метричному просторі 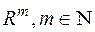 , але і тоді, коли розглядається стандартне продовження довільної міри
, але і тоді, коли розглядається стандартне продовження довільної міри 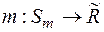 , визначеної на півкільці
, визначеної на півкільці 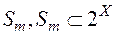 , при довільній непорожній множині
, при довільній непорожній множині 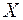 .
.
§1.9 Міра Жордана в 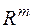
В математичному аналізі й інших розділах математики часто використовується міра, що будується наступним способом. Нехай 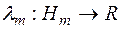 є міра на півкільці
є міра на півкільці 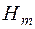 усіх піввідкритих паралелепіпедів із
усіх піввідкритих паралелепіпедів із 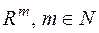 , що розглянута в попередньому параграфі. Міру, що є продовженням вказаної міри із півкільця
, що розглянута в попередньому параграфі. Міру, що є продовженням вказаної міри із півкільця 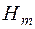 на кільце
на кільце 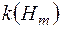 , також позначимо через
, також позначимо через 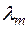 ,
, 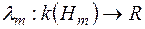 . Нагадаємо, що елементами кільця
. Нагадаємо, що елементами кільця 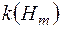 є всі найможливіші елементарні множини з
є всі найможливіші елементарні множини з 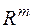 тобто всі найможливіші скінченні об’єднання піввідкритих паралелепіпедів із
тобто всі найможливіші скінченні об’єднання піввідкритих паралелепіпедів із 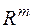 , які попарно не перетинаються (разом з порожньою множиною).
, які попарно не перетинаються (разом з порожньою множиною).
Означення Множина 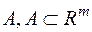 , називається вимірною за Жорданом, якщо
, називається вимірною за Жорданом, якщо 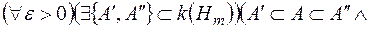
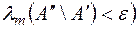 .
.
Позначимо 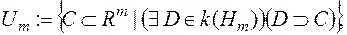
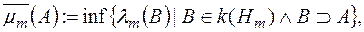
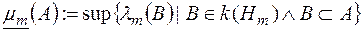 ,
,
де 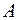 - довільна множина з класу
- довільна множина з класу 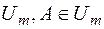 .
.
Числа 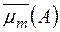 ,
, 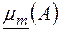 називаються відповідно значенням зовнішньої та внутрішньої міри Жордана множини
називаються відповідно значенням зовнішньої та внутрішньої міри Жордана множини 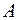 . Очевидно,
. Очевидно, 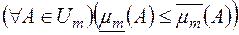 . Можна показати, що множина
. Можна показати, що множина 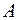 ,
, 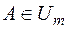 , вимірна за Жорданом тоді і лише тоді, коли
, вимірна за Жорданом тоді і лише тоді, коли 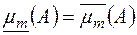 , і що сукупність
, і що сукупність 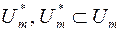 , усіх вимірних за Жорданом множин є кільце,
, усіх вимірних за Жорданом множин є кільце, 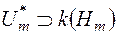 ,
, 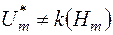 , яке не є
, яке не є 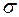 -кільце.
-кільце.
При цьому функція 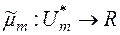 така, що
така, що 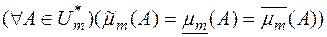 , є міра визначення на кільці
, є міра визначення на кільці 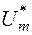 і вона є продовженням міри
і вона є продовженням міри 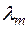 із півкільця
із півкільця 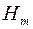 на кільце
на кільце 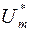 , тобто
, тобто 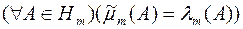 . Міра
. Міра 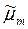 , вказана вище, називається продовженням міри
, вказана вище, називається продовженням міри 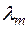 за Жорданом або мірою Жордана.
за Жорданом або мірою Жордана.
Можна показати, що кожна множина 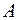 , яка вимірна за Жорданом,
, яка вимірна за Жорданом, 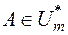 , є вимірна і за Лебегом ,
, є вимірна і за Лебегом ,  , причому значення лебегової і жорданової мір множини
, причому значення лебегової і жорданової мір множини 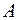 співпадають,
співпадають, 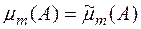 . Отже,
. Отже, 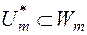 , де
, де 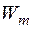 –
– 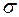 -алгебра усіх множин із
-алгебра усіх множин із 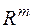 вимірних за Лебегом,
вимірних за Лебегом, 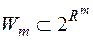 . Однак існують множини із
. Однак існують множини із 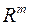 , що вимірні за Лебегом, але не вимірні за Жорданом, тобто
, що вимірні за Лебегом, але не вимірні за Жорданом, тобто 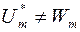 . Наприклад, множина
. Наприклад, множина 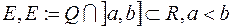 , вимірна за Лебегом, як зчисленна, але вона не є вимірною за Жорданом, оскільки
, вимірна за Лебегом, як зчисленна, але вона не є вимірною за Жорданом, оскільки 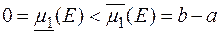 . Очевидно, множину
. Очевидно, множину 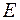 можна записати у вигляді
можна записати у вигляді 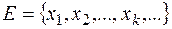 , де
, де 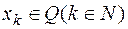 і
і 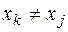 при
при 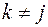 , тобто
, тобто  . Одноелементні множини
. Одноелементні множини 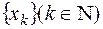 є вимірні за Жорданом, але їх об’єднання, яке дорівнює
є вимірні за Жорданом, але їх об’єднання, яке дорівнює 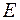 , не є вимірна за Жорданом множина. Це ще раз переконує в тому що, кільце
, не є вимірна за Жорданом множина. Це ще раз переконує в тому що, кільце 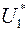 , не є
, не є 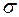 -кільце.
-кільце.
Дата добавления: 2015-07-24; просмотров: 1326;
