Поняття вимірної функції. Еквівалентні функції.
Нехай 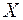 – довільна непорожня множина і
– довільна непорожня множина і 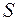 –
– 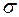 -алгебра множин,
-алгебра множин, 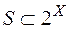 . Тоді впорядкована пара
. Тоді впорядкована пара  називається вимірним простором, а множини із
називається вимірним простором, а множини із 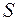 називаються вимірними. Якщо при цьому
називаються вимірними. Якщо при цьому 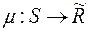 є міра на
є міра на 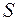 , то впорядкована трійка
, то впорядкована трійка  називається простором із мірою.
називається простором із мірою.
Нехай  та
та  – вимірні простори. Тоді відображення
– вимірні простори. Тоді відображення 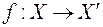 називається
називається 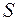 –
–  -вимірним, якщо
-вимірним, якщо 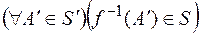 . При цьому, якщо
. При цьому, якщо  ,
,  , то
, то 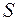 – –
– –  -вимірне відображення називається
-вимірне відображення називається 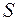 -вимірним. Отже, можна сформулювати наступне означення.
-вимірним. Отже, можна сформулювати наступне означення.
Означення 1. Нехай  – вимірний простір і
– вимірний простір і  – сігма-алгебра борелевих множин на
– сігма-алгебра борелевих множин на 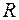 . Тоді функція (відображення)
. Тоді функція (відображення) 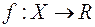 називається
називається 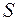 -вимірною, якщо
-вимірною, якщо  .
.
Очевидно, коли функція 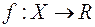 є
є 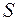 -вимірна, то множина
-вимірна, то множина 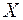 вимірна тобто
вимірна тобто 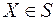 і кожна функція
і кожна функція 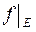 , де
, де  ,
, 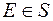 , є також
, є також 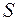 -вимірна.
-вимірна.
Зазначимо, що множини  ,
,  ,
, 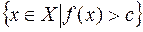 ,
, 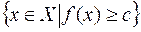 , де
, де  – довільне дійсне число називаються лебеговими множинами функції (відображення)
– довільне дійсне число називаються лебеговими множинами функції (відображення) 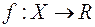 .
.
Попереднє означення, як можна показати, еквівалентне наступному означенню.
Означення 2. Функція 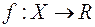 називається
називається 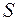 -вимірною, якщо
-вимірною, якщо 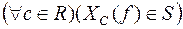 .
.
Очевидно, дістанемо рівносильні до попереднього означення, якщо в ньому замість  взяти будь-яку іншу лебегову множину.
взяти будь-яку іншу лебегову множину.
Якщо 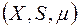 – простір із мірою
– простір із мірою  , визначеною на
, визначеною на 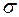 -алгебрі
-алгебрі 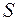 ,
, 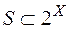 , то
, то 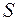 -вимірна функція
-вимірна функція 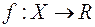 називається інакше
називається інакше  -вимірною або вимірною. Зокрема, якщо
-вимірною або вимірною. Зокрема, якщо 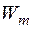 – сігма-алгебра всіх множин, вимірних за Лебегом,
– сігма-алгебра всіх множин, вимірних за Лебегом, 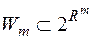
 і
і 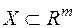 , то
, то 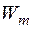 -вимірна функція
-вимірна функція 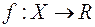 називається інакше вимірною за Лебегом.
називається інакше вимірною за Лебегом.
Очевидно, в загальному випадку функція 
 , що визначена на вимірній множині
, що визначена на вимірній множині  є
є 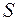 –вимірна. Можна також показати, що композиція
–вимірна. Можна також показати, що композиція  є вимірна функція, коли функція
є вимірна функція, коли функція 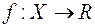 є
є 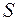 -вимірна, а функція
-вимірна, а функція  , де
, де 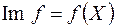 , неперервна. На основі цього доводиться, що функції
, неперервна. На основі цього доводиться, що функції 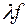 ,
,  (
( 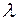 = const) є
= const) є 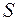 -вимірні на множині
-вимірні на множині 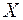 , якщо
, якщо 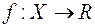 є
є 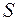 -вимірна функція
-вимірна функція 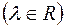 на
на 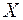 . Можна також показати, що
. Можна також показати, що 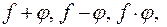
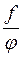 є
є 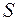 -вимірні функції на множині
-вимірні функції на множині 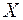 , якщо функції
, якщо функції 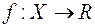 ,
, 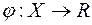 є
є 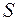 – –вимірні на
– –вимірні на 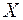 (при розгляді частки функцій додатково вимагається, щоб
(при розгляді частки функцій додатково вимагається, щоб 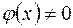 при
при  ).
).
Можна показати, що функція 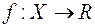 ,
, 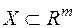 , вимірна за Лебегом, якщо вона неперервна на вимірній за Лебегом множині
, вимірна за Лебегом, якщо вона неперервна на вимірній за Лебегом множині 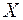 .
.
Нехай 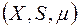 – простір із мірою
– простір із мірою 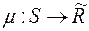 , визначеною на
, визначеною на 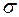 -алгебрі
-алгебрі 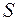 ,
, 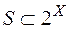 . Нехай
. Нехай  і
і  – така властивість, що кожен елемент
– така властивість, що кожен елемент  із
із 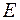 або володіє нею або не володіє. Тоді говорять, що властивість
або володіє нею або не володіє. Тоді говорять, що властивість  виконується майже скрізь на множині
виконується майже скрізь на множині 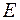 відносно міри
відносно міри  , якщо множина
, якщо множина 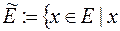 не володіє властивістю
не володіє властивістю  вимірна,
вимірна,  , і
, і  . Той факт, що властивість
. Той факт, що властивість  виконується майже скрізь на множині
виконується майже скрізь на множині 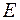 відносно міри
відносно міри  записують:
записують:  або
або  .
.
Означення3. При вказаних вище умовах функції  , де
, де  , називають еквівалентними на множині
, називають еквівалентними на множині 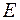 відносно міри
відносно міри  (або еквівалентними), якщо
(або еквівалентними), якщо  і
і  або інакше, коли
або інакше, коли 
 . Той факт, що функції
. Той факт, що функції 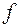 та
та 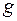 еквівалентні будемо записувати
еквівалентні будемо записувати 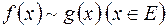 .
.
Очевидно, коли міра 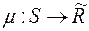 повна, функція
повна, функція 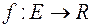 ,
,  , є вимірна і
, є вимірна і 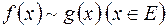 , то функція
, то функція 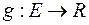 є також вимірна.
є також вимірна.
Дата добавления: 2015-07-24; просмотров: 1114;
