Властивості повних систем. Поняття замкненої системи

Визначення 4. Ортогональна система функцій 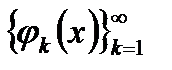з простору 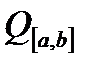називається замкненою, якщо з того, що функція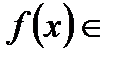 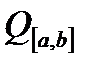ортогональна кожній функції з системи 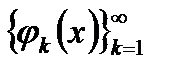витікає, що 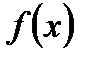~0 в просторі 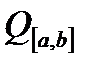, тобто 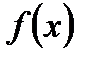може відрізнятися від 0 лише в скінченній кількості точок сегмента .

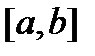Теорема 1. Якщо система 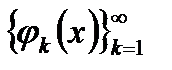є повною в просторі 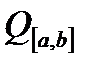, вона є і замкненою.

Доказ. Нехай функція 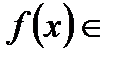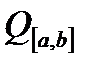ортогональна всім функціям .

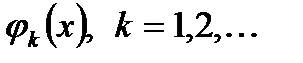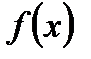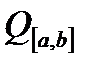Покажемо, що ~0 в . Маємо:

,

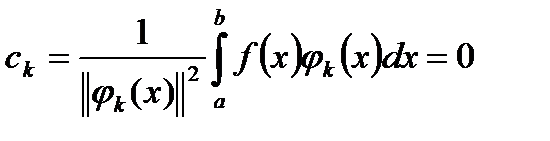бо 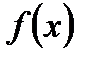ортогональна усім .

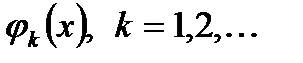Система 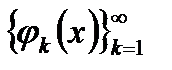є повною, тоді має місце рівність Парскваля: 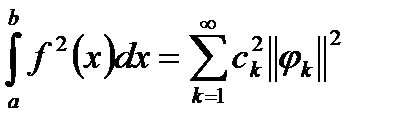. Враховуючи, що всі 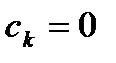, маємо:

,

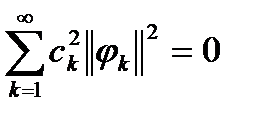а тому з рівності Парсеваля отримаємо:

,

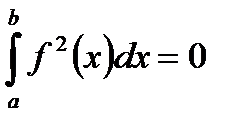звідки за властивістю визначеного інтегралу Римана витікає, що 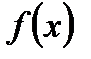~0, а тому система функцій є замкненою, що й потрібно було довести.

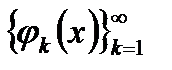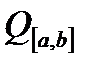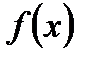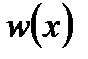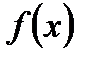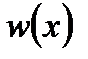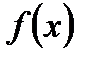Теорема 2. Якщо система функцій є повною в , а функції і мають однакові коефіцієнти Фурьє по цій системі, то ~ (якщо і 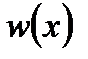- неперервні, то ).

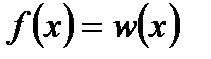Доказ. Побудуємо допоміжну функцію 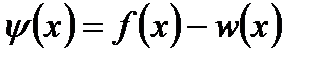. Знайдемо коефіцієнти Фурьє, для :

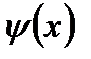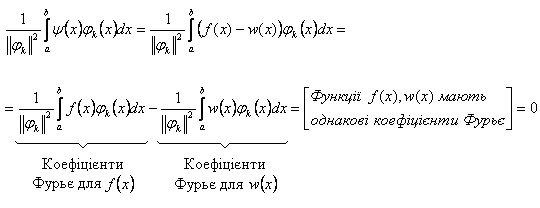
З того, що 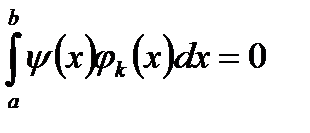для будь-якого 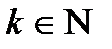витікає, що 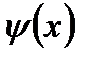ортогональна кожній 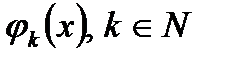. Оскільки 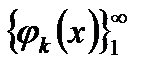повна, а тому і замкнена, то 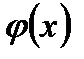~0, чи ~ .

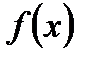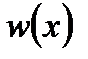Твердження. Основні тригонометричні системи є повними.

Питання

1. Коли кажуть, що функціональна послідовність 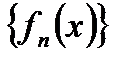збігається в середньому до 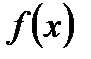з ?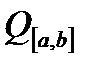

2. Коли кажуть, що функціональний ряд 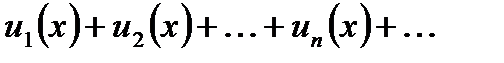збігається в середньому до суми ?

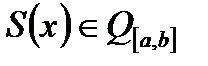3. Яка система ортогональних функцій 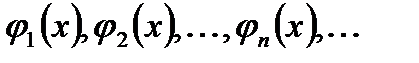з простору 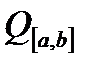називається повною в просторі ?

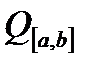4. Критерій повноти системи ортогональних функцій. Довести.

5. Яка ортогональна система функцій 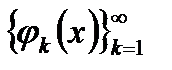з простору 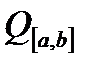називається замкненою?

6. Звязок між повнотою і замкненістю ортогональної системи.

7. Якими є основні тригонометричні системи?