Повна ортогональна система. Критерій повноти ортогональної системи. Рівність Парсеваля

Визначення 3. Система ортогональних функцій 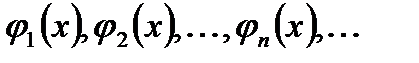з простору 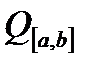називається повною в просторі 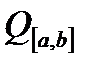, якщо ряд Фурьє для будь-якої функції 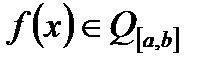збігається в середньому до .

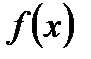Теорема 1 (критерій повноти системи ортогональних функцій). Ортогональна система 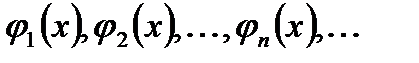буде повною в 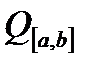тоді й тільки тоді, коли має місце рівність

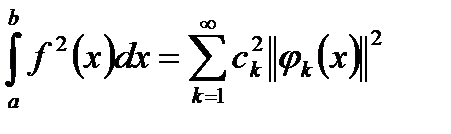для будь-якої .

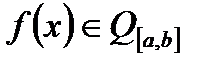Доказ. Нехай 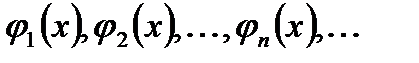- ортогональна система функцій в просторі 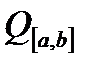. Побудуємо ряд Фурьє для довільної функції :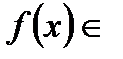

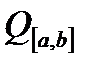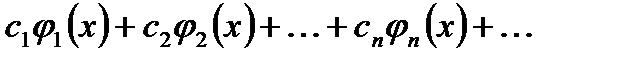, де .

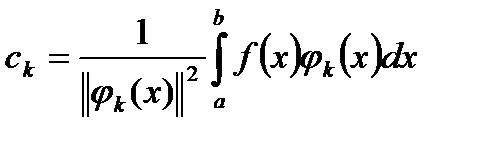За визначенням, система 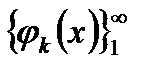є повною тоді й тільки тоді, коли 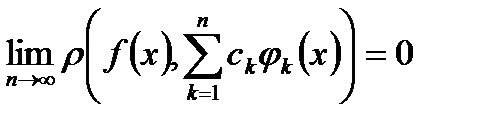, тут 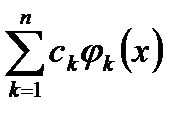- 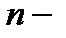а зрізана сума ряду 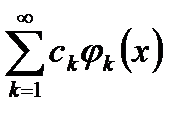, яка одночасно є многочленом Фурьє. Враховуючи це, згадаємо тотожність Бесселя:

.

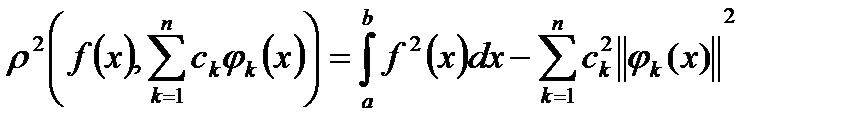Тоді, якщо перейти в лівій частині тотожності Бесселя до границі, коли 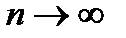, отримаємо:

,

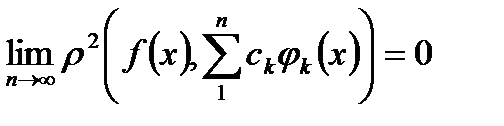але це рівносильно тому, що границя правої частини також дорівнює 0:

.

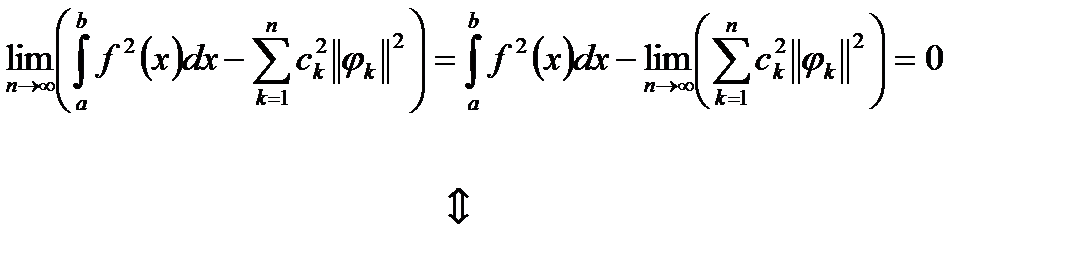
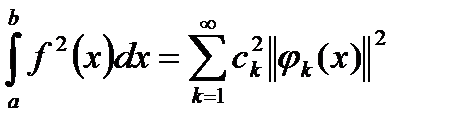Остання рівність має назву рівності Парсеваля.