Критерій Гурвіца

Для оцінки стійкості системи будується матриця Гурвіца з коефіцієнтами характеристичного рівняння.

По діагоналі заповнюємо таблицю, починаючи з a₁. У верхній половині вписуємо коефіцієнти, які зростають, а нижче діагоналі – з індексами, що спадають.

Для того, щоб система була стійкою необхідно і достатньо, щоб всі визначники матриці Гурвіца були додатні.

1. 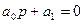(характеристичне рівняння)

a₀>0 D₁=a₀>0

2. 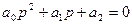(характеристичне рівняння)

a₀>0 D₁=a₁>0

3. 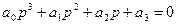(характеристичне рівняння)

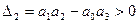
4. 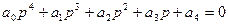(характеристичне рівняння)

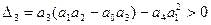
Недоліком критерію Гурвіца є складність обчислень для визначників високого порядку.

2.18. Частотні критерії стійкості

1. Критерій Михайлова (Кремера-Леонарда)

Випливає з наявності лівих коренів характеристичного рівняння.

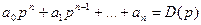
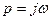
Відокремлюючи дійсну і уявну частину, поліном D(p) приводимо до виду:

D(p)=a(w)+jb(w)

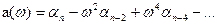– парні степені

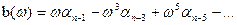– непарні степені

Геометричне місце точок кінця вектора D(jw) при зміні частоти 0<w<¥ називається годографом Михайлова.

Динамічна система, що описується лінійним диференційним рівнянням n-го порядку стійка, якщо при зміні частоти від 0 до ¥ годограф Михайлова послідовно проходить в напрямку проти годинникової стрілки n квадрантів комплексної площини і не перетворюється в 0.

Критерій Михайлова, зображений на рисунку, використовується для розімкнених систем управління.

Два наступних критерія, а саме – критерій стійкості Найквіста та логарифмічний критерій стійкості використовуються для оцінки на стійкість замкнутих систем управління.