Метод гармонічного балансу

Метод гармонічного балансу відноситься до наближених методів дослідження нелінійних систем. Він полягає у знаходженні розв’язку нелінійної системи виду Аsinwt, де А – амплітуда, w – частота.

Складну НДС можна звести до виду:

Запишемо умову Найквіста для такої системи:

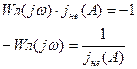
J 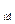(A) – еквівалентна амплітудо-фазова характеристика неінерційного нелінійного елементу. J 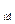(A) залежить від амплітуди і не залежить від частоти вхідної чи вихідної величин. Характеристика J 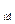(A) повністю визначається формою статичної характеристики НЕ.

J 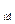(A) = N(A)+JM(A), де N(A) i M(A) – дійсна і уявна частина відповідно.

Коефіцієнти N(A) i M(A) визначаються як коефіцієнти ряду Фур’є.

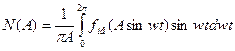
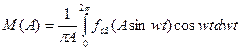
Для однозначних нелінійних характеристик M(A)=0.

Шукаємо точку перетину графіків -Wл(jw)

з 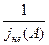(рис. 3.18).

Рис. 3.18.

З точок перетину графіків знаходять розв’язок А 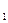sinw 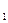t та А 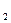sinw 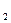t для точок C і D відповідно.

Список літератури до розділу 3:

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. Изд. 4-е, перераб. и доп. – СПб.: Изд-во “Профессия”, 2004. – 752с.

2. Сборник задач по теории автоматического регулирования и управления под редакцией В.А. Бесекерского. – М.: Наука, 1978. – 514с.

1. Нелинейные копчеева Ю.втоматического регулирования и управления под редакцией В.орректирующие устройства в системах автоматического управления. Под редакцией Топчеева Ю.И. – М.: Машиностроение, 1970.

2. Михайлов В.С. Теория управления. – К.: Высшая школа. Главное изд-во, 1988. – 312с.

3. Лозинський А., Мороз В., Паранчук Я. Розв’язування задач електромеханіки в середовищах пакетів MathCAD і MATLAB. Навч. посібник. – Львів: Вид-во Національного університету “Львівська політехніка”, 2000. – 166с.

4. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Спец. справочник. – СПб.: Питер, 2002. – 448с.

5. Мирошник И.В. Теория автоматического управления. Нелинейные и оптимальные системы. – СПб.: Питер, 2005 – 336с.

Розділ 4. Імпульсні дискретні системи управління