Логарифмічний критерій стійкості

Логарифмічний критерій стійкості використовується для замкнутих систем управління.

Логарифмічний критерій часто використовується при розрахунку коректуючих елементів.

ЛДС стійка в розімкнутому стані буде стійка і в замкнутому стані, якщо в діапазоні частот, де L(w)>0 значення фази j(w)>-p.

а) б) в)

а). Стійка система

б). Система на межі стійкості

в). Система нестійка

a –запас стійкості за фазою

Відображення випадків а), б) та в) логарифмічного критерію в годографі критерію Найквіста зображено на рис. 2.30.

Рис.2. 30.

2.19. Області стійкості

Під областю стійкості розуміють діапазони можливих змін параметрів налаштування (T_nⁿ,T₀,k) при яких система залишається стійкою.

Для визначення області стійкості систем 3-го порядку використовують діаграму Вишнєградського.

Для систем будь-якого порядку визначають стійкість за допомогою загального методу D-розбиття.

2.19.1. Метод D-розбиття

Виділення областей стійкості в площині параметрів ЛДС, яка описується диференційним рівнянням n-го порядку здійснюється на базі загального методу D-розбиття.

Для систем будь-якого порядку зручно використовувати критерій стійкості Михайлова. Коливній границі стійкості відповідає рівність нулю характеристичного комплекса D(jw) =0 (рис. 2.31).

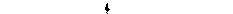
Рис. 2.31.

D-розбиття

Нехай 2 параметри А,В входять лінійно в характеристичний комплекс Аº(Т); Вº(К)

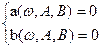
w – має значення чисто уявного кореня, або частоту гармонічних коливань в системі.

Повна сукупність всіх кривих в площині параметрів, що розбиває всю площину на області з пeвним розподілом коренів називається D-розбиття.

Приклад:

Розглянемо систему, у якої характеристичне рівняння має вигляд:

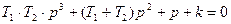
Побудувати область стійкості в площині параметрів Т 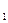і К.

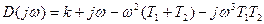
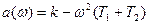– дійсна частина

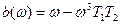– уявна частина

Шукаємо коливну границю:

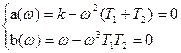
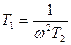
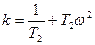
w	k	T1
		¥
…	…	…
¥	¥

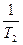
Таблиця визначення межі стійкості

для параметрів К i T Рис. Визначення області стійких

процесів для параметрів K i T

Правило штриховки.

Для нанесення штриховки знаходять знак визначника:

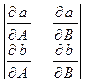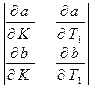/1/ /2/

Шукаємо 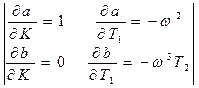/3/

D=-w³Т₂

Для частот від -¥ до 0 визначник додатний, тому при русі знизу вверх штрихуємо область зліва від кривої.

Область праворуч – область параметрів стійких процесів

2.20. Оцінка стійкості системи за її структурою

Якщо система має таку структуру, що неможливо забезпечити стійкість при будь-якій зміні параметрів, то така система називається структурно нестійка (рис. 2.32).

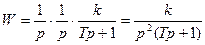
[С(р)+В(р)]×x_вих=0 Рис. 2.32.

С(р)+В(р)=0

p²(Tp+1)+k=Tp³+p²+k=0

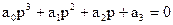
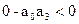
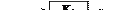Вводимо диференціюючу ланку для корекції (рис. 2.33):

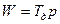
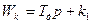
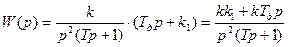Рис. 2.33.

B(p)+С (p)=0 – характеристичне рівняння для замкненої системи

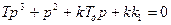
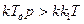– умова стійкості за Вишнєградським

Звідси ми можемо знайти співвідношення параметрів налаштування.

2.21. Стійкість систем при деяких комбінаціях окремих ланок

Рис. Годограф замкненої системи

2-го порядку

При будь-яких параметрах T₁,T₂,k₁,k₂ система буде стійкою.

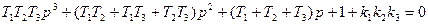
Коли ми застосуємо критерій Вишнєградського, то отримаємо, що коефіцієнт

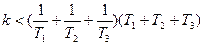
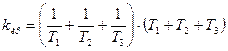
1. Стійка система k<k_кр

2. На межі стійкості k=k_кр (рис. 2.34)

3. Нестійка система k>k_кр Рис.2.34.

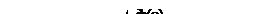
В даному випадку система зменшила стійкість (стала нестійкою) за рахунок фазового запізнення Dj.

Запізнення зменшує стійкість системи (рис. 2.35).

Рис. 2.35.

2.21.2. Комбінація інерційної і інтегруючої ланки

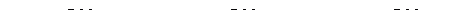
Рис. 2.36.

Введення інтегруючої ланки зменшує запас стійкості.

Введення диференціюючої ланки збільшує запас стійкості. Введення будь-якої ланки з відставанням зменшує запас стійкості, з випередженням – збільшує (рис. 2.36).

2.22. Якість управління в ЛДС

Під якістю управління розуміють характер перехідного процесу в системі, який виник через управляючі або збурюючі дії.

Якщо система не задовільняє необхідним показникам якості управління, то в неї вводять додаткові елементи – коректуючі пристрої, які, не порушуючи основного призначення системи, забезпечують необхідну якість управління.

Оцінки якості управління можуть бути:

1. Посередні (непрямі) – дозволяють отримати деякі параметри перехідного процесу, наприклад встановити принциповий характер (стійкий-нестійкий).

До посередніх оцінок відносять кореневі, інтегральні та частотні.

Кореневі – полягають в наявності зв’язку між формою h(t) і характером розподілу на комплексній площині коренів характеристичного рівняння.

Інтегральні – найбільш зручні для порівняльної оцінки.

Частотні – базуються на зв’язку між формою h(t) і дійсною частиною частотної характеристики.

Ці методи дозволяють приблизно нарисувати криву перехідного процесу не розв’язуючи диференційних рівнянь.

Прямі

Пряма оцінка може бути отримана тільки після побудови залежності h(t) чи х_вих(t) .

2.22.1. Побудова перехідних функцій систем управління частотним методом (метод зворотніх перетворень Лапласа)

Зв’язокh(t) замкненої системи управління з дійсною частиною АФЧХ a(w).

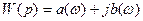
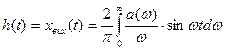- від дійсної частини

Аналогічним чином знаходять реакцію системи на одиничний стрибок, використовуючи уявну частину b(w).

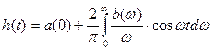- від уявної частини

2.22.2. Метод трапецій

Метод трапецій полягає у розбитті a(w) на ряд трапецій, кожна з трапецій буде мати розв’язок 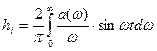і в результаті сумувань реакцій від кожної трапеції отримуємо загальне h(t), яке є сумою реакцій ряду трапецій.

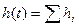
Для ЛДС це справедливо, оскільки їм притаманний принцип суперпозиції.

Даний метод є застарілим (табличним), тому використовується рідко.

2.22.3. Операторний метод (за допомогою розкладу Хевісайда)

Для знаходження h(t) необхідно знати корені знаменника передатної функції або так звані полюси (нулі знаменника).

Полюсом передатної функції є корені, коли знаменник рівний нулю.

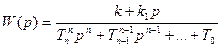
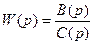
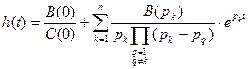
Вираз дозволяє побудувати перехідний процес в ЛДС при одиничній вхідній дії.

Операторний метод незручний для побудови перехідних процесів систем великого порядку. Найбільш ефективно цей метод застосовується тоді, коли маємо наявність коренів, а самої АФЧХ нема.

2.23. Корекція ЛДС

Може статися, що система (стійка або нестійка) не задовільняє вимогам динаміки, тобто є такою, що не забезпечує необхідних форм перехідних процесів. В таких випадках система доповнюється спеціальними коректуючими пристроями (КП). КП розрізняють послідовні і паралельні.

Паралельні КП є місцевими зворотніми зв’язками, які можуть бути як додатніми, так і від’ємними.

Визначення математичних моделей КП базується на використанні бажаних логарифмічних амплітудно-частотних характеристик L_баж(w). L_баж(w) відповідає ЛДС і повністю задовільняє вимогам до динамічних режимів.

Найбільший вплив на динаміку створює форма L_баж(w) в області частоти зрізу.

Розіб’ємо діапазон частот L_баж(w) на 3 частини (рис. 2.37):

0<w<w₁ – низькі частоти

w₂<w<w₃ – середні частоти

w₃<w – високі частоти

Побудова L_баж(w) починається з вибору w_зрізу, яке прямо зв’язано з швидкодією системи. Менші значення w_зрізу відповідають меншій швидкодії.

Рис. 2.37.

Аналіз систем, які мають високі динамічні якості вказує, що ЛАЧХ таких систем повинна мати в районі частоти зрізу нахил в районі 20 дБ/дек.

Характеристика правіше точки D залишається такою, як у початковій системі.

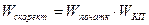
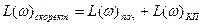
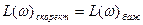
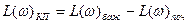
Отже, для визначення логарифмічної характеристики коректую чого поліному, необхідно здійснити віднімання від значень L(w) 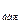значень L(w)

Список літератури до розділу 2:

1. Попович М.Г., Ковальчук О.В. Теорія оатоматичного керування. – К., 1997.

2. Никулин Е.А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем. Учеб. пособие для вузов. – СПб.: БХВ – Петербург, 2001. – 640с.

3. Валюх О.А., Максимів В.М. Елементи теорії автоматичного керування. Лінійні системи неперервної дії. Навч. посібник. – Львів: Афіша, 2001. – 124с.

4. Мирошник И.В. Теория автоматического управления. Линейные системы. – СПб.: Питер, 2005 – 336с.

Розділ 3. Нелінійні системи управління

Нелінійними називаються системи, які містять нелінійний елемент, тобто такі, у яких відношення “вхід-вихід” описується нелінійними рівняннями.

Строго кажучи, всі елементи є нелінійні, тому лінійні методи аналізу і синтезу лінійних систем не можуть використовуватись.

В цілому теорія НДС є більш складної і менш розробленою. Це пояснюється великою різноманітністю типів нелінійних систем. Велике коло нелінійних систем містить нелінійні елементи з типовими нелінійностями.

Нелінійні елементи у яких 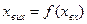однакова при зростанні і спаданні х_вх називаються нелінійностями з однозначними статичними характеристиками. /рис. а, б/

3.1. Типові нелінійності

1.Обмеження (насичення)

Аналітичний вираз

а). -В,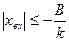

б). kx_вх,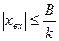

в). В,

2. Нечутливість

а). х_вих=0 при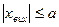

б). х_вих=-ka+kx_вх при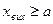

в). х_вих=ka-kx_вх при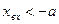

3. Релейна

а). х_вих=-В при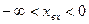

б). х_вих=В при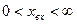

4. “Гістерезис”

а). х_вих=-ka+kx_вх при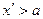

б). х_вих=ka-kx_вх при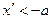

в). при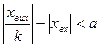

3.2. Властивості нелінійних систем

Характер можливих рухів в нелінійних системах (НС) більш широкий, ніж в лінійних. В лінійних системах рух може бути або такий, що сходиться, або такий, що розходиться (рис. 3.1).

Існування стійких коливань в ЛДС недопустиме, оскільки це означає знаходження системи на межі стійкості. Такий режим роботи в ЛДС практично неможливий.

В НС можливі стійкі коливання при відсутності зовнішніх періодичних збурень – такі рухи називаються автоколиваннями, а системи називаються автоколивальні.

Амплітуда і частота автоколивань визначається параметрами системи. В одній НС можуть бути кілька режимів автоколивань.

Природа виникнення автоколивань в НС зв’язана з тим, що коефіцієнт підсилення НС на різних ділянках статичної характеристики різний, що зумовлює автоматичний перехід від рухів, що розходяться до рухів, що сходяться і навпаки (рис. 3.2).

Рис. 3.1. Рис.3.2.

В НС змінюється постановка і вирішення задачі аналізу стійкості. Якщо в ЛДС стійкість залежить тільки від властивостей системи і не залежить від змінних в початковий момент в НС, котрі є стійкими при малих відхиленнях можуть виникати нестійкі режими при великих початкових відхиленнях.

Тому для НС вводять поняття “стійкість в малому” і “стійкість у великому”.

3.3. Методи дослідження НДС.

Точні розв’язки нелінійних систем управління можуть відноситися до систем не вище другого-третього порядку.

Способів розв’язку нелінійних систем є досить багато, крім того вони можуть застосовуватись в модифікаціях при розв’язку конкретних нелінійних систем.

Ми розглядаємо 2 основних способи розв’язку НС:

1. Метод фазових траєкторій – відноситься до точних розв’язків динамічних систем.

2. Метод гармонічного балансу – відноситься до наближених методів розв’язку.

3.3.1. Метод фазових траєкторій

Для наочного зображення складних процесів управління застосовують поняття фазового простору, яке полягає в наступному: диференційне рівняння замкнутої системи n-го порядку приводиться до системи n рівнянь першого порядку.

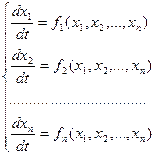
Рис. 3.3.

M₀ – зображаюча точка, а траєкторія руху точки M₀ називається фазовою траєкторією, а простір х₁х₂х₃ – фазовий простір (рис. 3.3).

Фазовий простір і фазові траєкторії представляють собою геометричний образ динамічних процесів.

Якщо рівняння складені у відхиленнях від встановленого значення, то х₁=х₂=х₃ =0, для стійких систем при t→∞.

Отже, зображенням встановленого стану системи є початок координат фазового простору. Звідси випливає, що фазові траєкторії стійкої системи будуть асимптотично наближатися до нуля при необмеженому збільшенні часу. Фазові траєкторії нестійкої системи будуть необмежено віддалятись від початку координат.