Дискретні системи управління
Дискретними називаються системи, в яких змінні, що характеризують систему, мають переривчастий дискретний характер.
Характерною рисою будь-якої дискретної системи є наявність імпульсного елементу (ІЕ), за допомогою якого здійснюється перетворення неперервних величин в послідовність дискретних сигналів – імпульсів.
4.1.1. Переваги дискретних систем (ДС) управління
1. Збільшена завадостійкість
2. Збільшена точність управління, оскільки завади в ДС діють тільки в дискретні моменти.
3. Збільшена ефективність передачі сигналів управління.
ДС можуть бути як замкнуті, так і розімкнуті. Сучасна теорія управління користується методом дослідження ДС – дискретним перетворенням Лапласа.
ДС можуть бути як лінійні, так і нелінійні.
ДС, які реалізують сигнали, квантовані по часу називаються імпульсними системами(рис. 4.1).
 |
ДС, які реалізують сигнали, квантовані і по рівню і по часу називаються цифровими або релейно-імпульсними (рис. 4.2).
Рис. 4.1. Рис. 4.2.
4.1.2. Математичний опис систем дискретного управління
Решітчатою функцією називається функція, яка отримується в результаті заміни неперервної змінної дискретною залежною змінною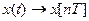 
і визначена в дискретні моменти часу – nT, (n+1)T.
Аргумент решітчатої функції Т доречно представити так, щоб відлік по шкалі часу вести в цілих одиницях періоду квантування.
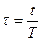
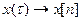
Зв’язок між значеннями решітчатої функції при різних значеннях аргумента визначається за допомогою різниць, які є аналогами похідних в диференційних рівняннях.
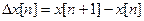
Dx – характеризує швидкість зміни решітчастої функції
D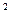 
x – визначається як різниця двох сусідніх похідних.
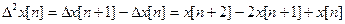
За аналогією можемо записати вираз для m-ї різниці (похідної m-го порядку).
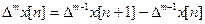
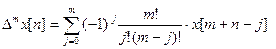
Математична модель імпульсної системи зводиться до виду:
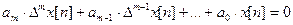/1/,
де а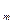 
- постійні коефіцієнти
Рівняння /1/ є аналогом однорідного лінійного диференційного рівняння, яке застосовується в описі неперервних систем управління.
Розв’язок системи /1/ дає значення змінної x[n] для кожного періоду квантування.
Використовуючи зв’язок різниць з дискретними значеннями решітчастої функції рівняння /1/ можна записати у виді:
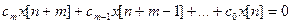/2/
або 
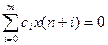/3/
Рівняння /2/ або /3/ дозволяють при відомих значеннях x[0], x[1], … , x[n] послідовно визначити значення x[0+m], x[1+m], … , x[n+m].
Подібно до того, як в теорії безперервних лінійних систем для розв’язку диференційних рівнянь використовувалось перетворення Лапласа, в теорії імпульсних систем для розв’язку різницевих рівнянь використовується дискретне перетворення Лапласа і його модифікація – дискретне z-перетворення.
Якщо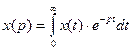 
перейдемо від безперервної функції x(t) до дискретної x[nT), де t=nT. При цьому інтеграл переводиться в суму, а сума приростів по часу відобразиться періодом квантування Т.
Тоді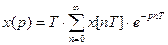 
.
Якщо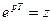 
, то отримаємо 
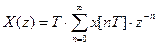/4/
Вираз /4/ - це дискретне перетворення Лапласа, в якому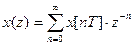 
називається z-перетворенням.
4.2. Передатна функція імпульсних систем
Відношення z-перетвореної вихідної величини до z-перетвореної вхідної величини при нульових початкових умовах називається дискретною передатною функцією.
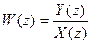
Рис. 4.3.
Дискретна передатна функція імпульсної системи з фіксуючим елементом (ФЕ) (рис. 4.3) має вигляд:
,
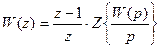де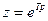 
- комплексна змінна
Z – символ-z-перетворення
W(p) – передатна функція безперервної частини (НЧ).
4.3. Стійкість імпульсних систем
Загальний вигляд рівняння руху імпульсної системи, що знаходиться під впливом вхідної дії.
/1/
Тоді, в розгорнутому вигляді рівняння /1/ буде:
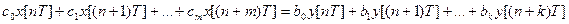/2/
Загальний розв’язок рівняння:
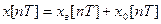/3/
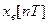– вимушений рух системи; 
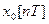– вільний (власний) рух системи
Про стійкість судять за власним рухом системи, отже:
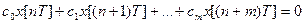/4/
Розв’язок цього рівняння будемо шукати у вигляді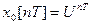 
, 
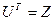, тобто 
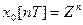з врахуванням /4/ має вигляд:
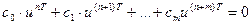
Після скорочення на uT отримаємо:
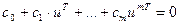/5/
Позначивши uT=Z, отримаємо характеристичне рівняння вільного руху імпульсної системи.
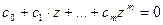/6/
Розв’язок рівняння /6/має вигляд:
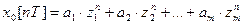/7/
– корені характеристичного рівняння
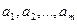– постійні коефіцієнти, що визначаються з початкових умов.
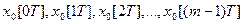
Розв’язок рівняння /7/буде сходитися, а система, що має характеристичне рівняння /6/ буде стійкою, якщо
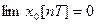/8/
Ця умова виконується тоді, коли кожен доданок /7/задовільняє умові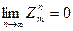 
, а це буде тоді, коли всі корені по модулю менші одиниці.
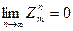при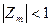 
Таким чином, необхідною і достатньою умовою стійкості імпульсної системи є умова 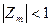для всіх коренів характеристичного рівняння, що відповідає різницевому рівнянню системи.
Враховуючи, що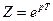 
, перетворимо площину комплексної змінної р в комплексну площину коренів z (рис.4.4).
Рис. 4.4.
Дата добавления: 2015-07-24; просмотров: 2794;