Асиметричні (відкриті) криптосистеми

Криптографічні системи з відкритими ключами шифрування дозволяють користувачам здійснювати безпечну передачу даних по незахищеному каналу без будь-якої попередньої підготовки. Такі криптосистеми повинні бути асиметричними в тому сенсі, що відправник і по одержувача мають різні ключі, причому жоден з них не може бути виведений з іншого за допомогою обчислень.

У цих системах фази шифрування і дешифрування, і захист повідомлення забезпечується без засекречування ключа шифрування, оскільки він не використовується при дешифруванні. Тому ключ публікується разом з алгоритми шифрування і дешифрування, і це не приносить шкоди захисті системи. Принцип функціонування системи з відкритими ключами шифрування полягає в наступному: користувач i шифрує повідомлення М, використовуючи відкритий ключ шифрування користувача j, і посилає шифроване повідомлення користувачеві j по незахищеному каналу передачі даних. Тільки користувач j може виконати дешифрування, щоб відновити М, оскільки тільки він знає секретний ключ дешифрування. Алгоритми шифрування Е (Encryption) і дешифрування D (Decryption) в таких системах характеризуються наступними властивостями [RIVE78]:

Властивість 1. Дешифрування шифрованого повідомлення відновлюється вихідне повідомлення М, тобто

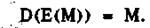
Властивість 2. Алгоритми шифрування Е і дешифрування D є простими в реалізації.

Властивість 3. При розкритті алгоритму шифрування Е ал горітм дешифрування D не розкривається, тобто тільки підлозі отримувача або відправник можуть дешифрувати повідомлення, за шифрування алгоритмом Е, тобто виконати алгоритм де шифрування D.

Властивість 4. Якщо повідомлення М спочатку дешифровано, а потім зашифровано, то справедливо умова

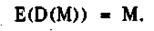
Властивість 4 не обов'язково для систем з відкритими ключами, але якщо воно виконується, то можна використовувати цифрові сигнатури.

Криптографічні системи з відкритими ключами використовують функції шифрування, що володіють властивістю одно спрямованість. Це властивість встановлює умова, яка вимагає, щоб захищений ключ не можна було відновити по відкритому ключу. Однонаправлені функції характеризуються наступними властивостями:

1. Як функція у = f (x), вона обчислюється просто.

2. Має зворотну функцію.

3. Зворотну функцію вкрай складно вирахувати.

Визначення односпрямованої функції включає поняття складності, яке залежить від обчислювальних можливостей комп'ютерів. Ступінь складності оцінюється в витратах часу, необхідного обсягу пам'яті або твори цих величин.

Оскільки законний одержувач повинен мати можливість дешифрувати повідомлення, то в системах з відкритими ключами слід використовувати односпрямовані функції з обхідними шляхами, що володіють додатковим властивістю: зворотна функція не повинна бути обчислюваною, якщо невідома спеціальна інформація про обхідних шляхах.

Криптографічна система RSA (Rivest-Shamir-Adleman)

Обхідний шлях в асиметричної схемою системи RSA основана на заміні процедури знаходження великих простих чисел процедурою їх розкладання на множники.

Принцип, системи RSA, можна описати таким чином. Одержувач вибирає два великих простих числа p і qтак, щоб твір n = pq знаходилося за межами обчислювальних можливостей. Вихідне повідомлення М може мати довільну довжину в діапазоні 1 <М <п. Шифрований текст С, відповідне повідомленням М, може бути отриманий з перестановки.

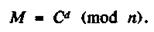
Алгоритм шифрування RSA-методом наступний:

Крок 0: Задати вхідну послідовність

input

Крок 1: Нехай - двійкове подання числа e

Крок 2: Встановити С = 1

Крок 3: Повторювати кроки 3а та 3б для i = k ... 1,0

3а: Присвоїти З значення залишку від ділення С2 на n

3б: Якщо ei = 1, то привласнити З значення залишку від ділення З input на n

Крок 4: Зупинка. З-шифрований текст входу input.

Порядок дешифрування наступний:

Одержувач вибирає e і d так, щоб виконувались умови:

а) НОД (е, Ф (n)) = 1;

б) ed = 1 (mod Ф (n)) де

Ф (n) - функція Ейлера (p-1) (q-1)

НСД (a, b) - найбільший спільний дільник двох чисел;

Робота схеми шифрування-дешифрування заснована на теоремі Ейлера, яка встановлює, що для будь-якого цілого М, взаємно простого з n, справедливо

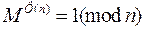
Використовуючи умову б) отримаємо для деякого цілого K

Для всіх M, не діляться на p, виконується порівняння

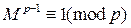
Оскільки Ф (n) кратно (p-1), справедливо

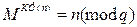
Коли 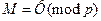, то попереднє рівняння виконується тривіально. За аналогією, для q справедливо

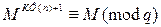
По теоремі залишків для всіх М справедливо

У цій системі числа е і п є несекретними і визначають ключ шифрування. Числа d, p, і q зберігаються секретними і визначають ключ дешифрування. Якщо п легко розкладається на множники р і q, то криптоаналітика знайде F (n), а потім d і розкриє систему шифрування

Вибір показників ступеня при кодуванні

Вибравши прості числа р і q, а отже, і п, необхідно приступити до вибору показників ступеня eіd. Для цього d вибирається з умови, щоб воно було взаємно простим з Ф (n). Це досягається обчисленням залишку d (mod n) і НОД (d, Ф (і)) з допомогою алгоритму Евкліда. Алгоритм дозволяє не тільки перевірити, чи є числа d і Ф (п) взаємно простими, але також підрахувати мультиплікативно - зворотний до d показник ступеня тобто Відомо, що складність обчислення функції HОД має тимчасову оцінку O (log2n) [KNUT81]. На вибір показників е до d необхідно подати умову, щоб ці величини перевищували log2n. Якщо е <log2n, то малі повідомлення виявляться незашифрованими.

Якщо буде виконуватися умова, то шифр розкривається простим перебором. Якщо d <log2n, то система може бути розкрита тільки випадково.

Існує ще одна умова при виборі тобто Як уже згадувалося, щоб здійснити перестановки у повідомленні згідно з функцією е, е повинно бути взаємно простим з функцією Ейлера Ф (n), або,

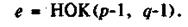
більш точно, взаємно простими з НОК - найменшим спільним кратним наступних числу:

Серед цих перестановок є й такі, які зберігають повідомлення, і вони задовольняють умові конгруентності

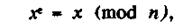
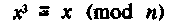
де е - непарне число, більше 3, і n = рд. Відомо, що будь-яке рішення рівняння

задовольняє і першому рівнянню. Далі відзначимо, що друге рівняння має 9 рішень в діапазоні чисел 1 <х <п-1 (n = pq).

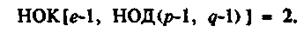
Таким чином, перше рівняння має щонайменше 9 рішень. Можна показати, що рівняння конгруентності буде породжувати рівно 9 рішень, якщо показник ступеня буде обраний з