Криптографічний аналіз RSA-системи

Ймовірно, головною метою криптографічного розкриття є визначення секретного показника ступеня d. Відомі три способи, якими міг би скористатися криптоаналітик для розкриття величини d по відкритій інформації j

парі (е, n).

Факторизація п

Розкладання величини п на прості множники дозволяємо обчислити функцію Ф (n) і, отже, приховане значення d, використовуючи рівняння.

Найбільш швидкий алгоритм, відомий в даний час може виконати факторизацію n за число кроків порядку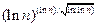

Обчислення Ф (п) без факторизації

Інший можливий спосіб криптоаналізу пов'язаний з безпосереднім обчисленням функції Ейлера Ф (n) без факторизації п. В роботі [RIVE78] показано, що пряме обчислення Ф (п) анітрохи не простіше факторизації п, оскільки Ф (п) дозволяє після цього легко факторизувати п. це можна бачити

з наступного прикладу. Нехай

Знаючи Ф (n), можна визначити х і, отже, у; знаючи х і у, прості р і q можна визначити з наступних співвідношень

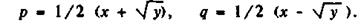
Пряма оцінка d без факторизації п або обчислення Ф (n)

Третій спосіб криптоаналізу полягає у безпосередньому обчисленні величини d. Аргументація цього способу заснована на тому, що якщо d вибрано досить великим, щоб простий перебір був неприйнятний, обчислення d не простіше факторизації і якщо d відомо, то п легко факторізується. Це можна показати наступним чином. Якщо d відомо, то можна обчислити величину, кратну функції Ейлера, використовуючи умову

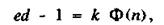
де k - довільне ціле число.

Факторизацію п можна виконати, використовуючи будь-яке значення, кратне F (n). Дешифрувальник, з іншого боку, може спробувати знайти деяку величину d ', яка була б еквівалентна прихованої величині d, використаної при розробці шифру. Якщо існує багато таких d ', то можна спробувати використовувати прямий перебір, щоб розкрити шифр. Але все d 'розрізняються множником, рівним НОК (р-1, q-1), і якщо цей множник обчислений, то п можна факторизувати. Таким чином, знаходження d настільки ж складно, як і факторизація п.