Фазові портрети систем
1. Фазовий портрет (рис. 3.4) консервативної системи (системи на межі стійкості).
Система має тільки уявні корені p 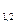 =±jβ. В цьому випадку маємо незгасаючі коливання (рис. 3.5)
=±jβ. В цьому випадку маємо незгасаючі коливання (рис. 3.5)

Рис. 3.4. Рис. 3.5.
2. Фазовий портрет стійкої системи 2-го порядку.


 |
Система має від’ємні дійсні корені Re p
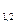 =α<0 (рис. 3.6). В цьому випадку маємо загасаючий коливальний перехідний процес, фазові траєкторії сходяться до положення рівноваги (рис. 3.7).
=α<0 (рис. 3.6). В цьому випадку маємо загасаючий коливальний перехідний процес, фазові траєкторії сходяться до положення рівноваги (рис. 3.7).
Рис. 3.6. Рис. 3.7.
3.  Фазовий портрет нестійкої системи 2-го порядку
Фазовий портрет нестійкої системи 2-го порядку
Система має дійсні додатні корені Re p 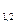 =α >0 (рис. 3.8).
=α >0 (рис. 3.8).
Рис. 3.8. Рис. 3.9.
3.3.3. Особливі точки фазових траєкторій
 |
 |
Рис. 3.10.
Для динамічних нелінійних систем можливі стійкі автоколивання, тобто значення змінних можуть періодично повторюватись. Ця можливість приводить до появи замкнених циклів, які називаються граничними циклами (рис. 3.11).

Рис. 3.11.
Для визначення стійкості граничного циклу необхідно нарисувати дві фазові траєкторії: одну всередині циклу, іншу – за межами циклу і прослідкувати рух точки всередині траєкторій.
3.4. Поняття стійкості за Ляпуновим
Незбурений рух (встановлений процес) називається стійким, якщо при заданій як завгодно малій області e можливо знайти таку область h, що при початкових умовах, розміщених всередині цієї області, збурений рух – перехідний процес буде таким, що зображаюча точка не вийде з області h при як завгодно великому значенні часу t (рис. 3.12).
Рис. 3.12.
3.5. Розв’язок нелінійних динамічних систем (методом фазових траєкторій)
Лінії перемикань є геометричним місцем точок фазової площини, де здійснюється перехід від одного лінійного диференційного рівняння до фазових траєкторій другого лінійного диференційного рівняння (рис. 3.13).

Рис. 3.13.
Лінії перемикань диференційних рівнянь відповідатимуть точкам статичних характеристик A, B і C, D (рис. 3.13).
Як приклад, розглянемо систему регулювання температури ОУ пропарочної камери (рис. 3.14).

Рис. 3.14.
ПР – поляризоване реле
К.Пр – контакти ПР
U 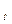 - напруга живлення мостової схеми
- напруга живлення мостової схеми
ОЗ1, ОЗ2 –обмотки збудження двигуна Д
R 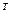 – терморезистор
– терморезистор
В – вентиль (регулятор)
Рівняння об’єкту управління системи буде виглядати наступним чином:
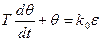
або
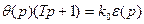
Рівняння руху двигуна:
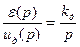
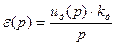
Структурна схема, що відповідає написаним рівнянням динаміки з врахуванням характеру нелінійності буде виглядати як зображено на рис. 3.15:

Рис. 3.15.
 Об’єднуючи лінійні ланки в одну лінійну частину, отримуємо схему, зображену на рис. 3.16:
Об’єднуючи лінійні ланки в одну лінійну частину, отримуємо схему, зображену на рис. 3.16:
Рис. 3.16.
Рівняння лінійної частини системи матиме наступний вигляд:
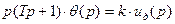 де
де 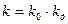
Рівняння руху системи розіб’ється на три диференційні рівняння 2-го порядку:
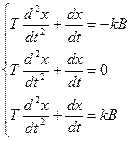 (1)-(3)
(1)-(3)
Для побудови фазового портрету вибиремо координати фазової площини х та 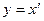 . Тоді рівняння (2) запишеться:
. Тоді рівняння (2) запишеться:
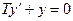 або
або 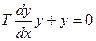 , тобто
, тобто 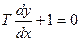 Þ
Þ 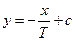





Рис. 3.17.
Тоді розв’язок рівняння (1) та розв’язок рівняння (3) із системи буде:
 для (2)
для (2)
для (1)
для (3)
Фазовий портрет системи, згідно розв’язків, зображений на рис. 3.17.
Дата добавления: 2015-07-24; просмотров: 2230;
