Доказательство. - нулевая как сумма нулевых ф.п.р.ч.

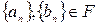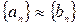Пусть и . Тогда 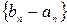- нулевая.

1. 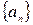- нулевая.

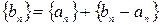- нулевая как сумма нулевых ф.п.р.ч.

2. 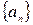- положительная.

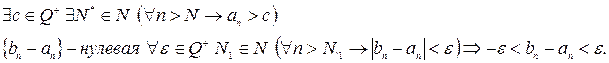Возьмем . Тогда получим

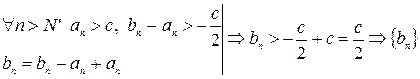- положительная.

3. 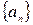- отрицательная.

Нетрудно проверяется, что 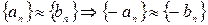. Тогда 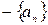- положительная, следовательно, согласно пункту 2 этой теоремы 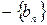- положительная, а, значит, 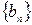- отрицательная ф.п.р.ч.

что и требовалось доказать

Теорема 8.Отношение ≈ стабильно относительно операции сложения, умножения и взятия противоположного на множестве всех фундаментальных последовательностей рациональных чисел.