Доказательство. Пусть . Тогда и - нулевые ф.п.р.ч.

Пусть 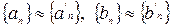. Тогда и - нулевые ф.п.р.ч.

Отношение ≈ стабильно относительно операции сложения (?)

Поскольку сумма нулевых последовательностей является нулевой, имеем 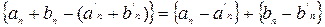- нулевая ф.п.р.ч., а значит .

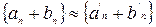Отношение ≈ стабильно относительно операции умножения (?)

Последовательности 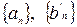фундаментальные, следовательно, ограниченные, предположим, числами соответственно. Зная, что и нулевые ф.п.р.ч. имеем

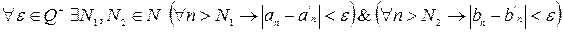. Выберем . Тогда . Принимая во внимание выше перечисленное, оценим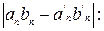

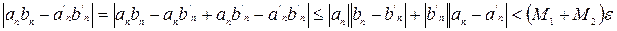. Последнее влечет, что 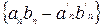является нулевой, а, значит, .

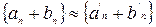Отношение ≈ стабильно относительно операции взятия противоположного (?)

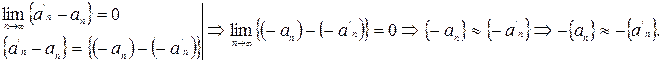что и требовалось доказать