Решение. Имеем . Отсюда , . Подставим данные выражения в уравнение окружности и получим
Имеем 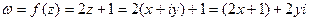 . Отсюда
. Отсюда 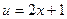 ,
, 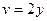
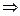
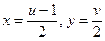 . Подставим данные выражения в уравнение окружности и получим
. Подставим данные выражения в уравнение окружности и получим 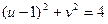 . Следовательно, искомым отображением является окружность с радиусом 2 и с центром в точке (1, 0).
. Следовательно, искомым отображением является окружность с радиусом 2 и с центром в точке (1, 0).
2. Простейшая дробно-линейная функция 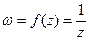 .
.
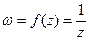 – аналитическая функция, т.к. выполняются условия КРЭДа.
– аналитическая функция, т.к. выполняются условия КРЭДа. 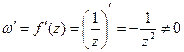 ни при каком конечном z (лишь при
ни при каком конечном z (лишь при 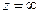 ). Следовательно, производная существует всюду, кроме z = 0.
). Следовательно, производная существует всюду, кроме z = 0.
Отображение, реализуемое функцией, конформно всюду на 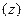 , кроме точки z = 0 и бесконечно удаленной точки
, кроме точки z = 0 и бесконечно удаленной точки 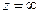 . Если положить
. Если положить 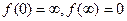 , то отображение будет конформно во всей плоскости
, то отображение будет конформно во всей плоскости 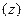 . При этом угол между прямыми в точке О отображается на такой же угол в бесконечно удаленной точке
. При этом угол между прямыми в точке О отображается на такой же угол в бесконечно удаленной точке 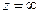 .
.
Геометрический смысл отображения.
Пусть 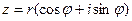 , тогда его образ можно найти по формуле Муавра
, тогда его образ можно найти по формуле Муавра 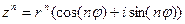 , т.е.
, т.е. 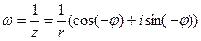 . Видно, что 1)
. Видно, что 1) 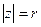 , а
, а 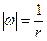 , 2)
, 2) 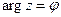 , а
, а 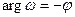 (рис. 23). Отсюда можно сделать вывод: отображение
(рис. 23). Отсюда можно сделать вывод: отображение 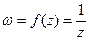 может быть представлено в виде двух составляющих: 1)
может быть представлено в виде двух составляющих: 1) 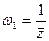 и 2)
и 2) 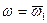 . Разберем подробнее каждую составляющую.
. Разберем подробнее каждую составляющую.
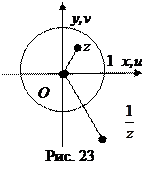 1) Окружность радиуса r отображается с помощью функции
1) Окружность радиуса r отображается с помощью функции 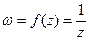 в окружность радиуса
в окружность радиуса 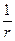 , т.е., если точка z лежит внутри единичной окружности на плоскости (Oxy) , то ее образ, точка
, т.е., если точка z лежит внутри единичной окружности на плоскости (Oxy) , то ее образ, точка 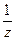 , лежит вне единичной окружности на плоскости (Ouv). Все точки окружности отображаются в себя, т.е. остаются на месте; концентрические окружности радиуса < r переходят в окружность радиуса > r и обратно. Точки 0 и
, лежит вне единичной окружности на плоскости (Ouv). Все точки окружности отображаются в себя, т.е. остаются на месте; концентрические окружности радиуса < r переходят в окружность радиуса > r и обратно. Точки 0 и 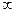 переходят друг в друга.
переходят друг в друга.
Определение 39. Преобразование, переводящее внутренность единичного круга во внешность и наоборот, называется инверсией.
То есть инверсия – зеркальное отображение плоскости z относительно окружности.
Свойство инверсии: при инверсии все окружности, а также прямые преобразуются в окружности или в прямые, причем окружность, равно как и прямая, может преобразоваться либо в окружность, либо в прямую. Вообще говоря, инверсия представляет собой антиконформное отображение.
Из отображения 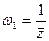 следует, что
следует, что 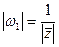 ,
, 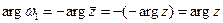 . Поскольку
. Поскольку 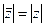 , то
, то 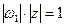 (*).
(*).
 Определение 40. Точка
Определение 40. Точка 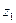 называется симметричной точке
называется симметричной точке 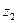 относительно окружности
относительно окружности 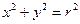 , если данные точки лежат на одном луче и
, если данные точки лежат на одном луче и 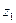 ∙
∙ 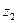 =
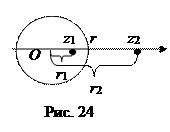
= 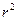 (рис. 24). Точки называются симметричными относительно окружности единичного радиуса с центром в начале координат, если они расположены на одном луче, а произведение длин их радиус-векторов равно единице.
(рис. 24). Точки называются симметричными относительно окружности единичного радиуса с центром в начале координат, если они расположены на одном луче, а произведение длин их радиус-векторов равно единице.
Следовательно, из определения 40 и из (*) следует, что функция 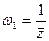 отображает любую точку, лежащую внутри единичного круга в симметричную ей точку относительного данной окружности, лежащую вне единичного круга и обратно, т.е
отображает любую точку, лежащую внутри единичного круга в симметричную ей точку относительного данной окружности, лежащую вне единичного круга и обратно, т.е 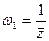 – инверсия относительно единичной окружности.
– инверсия относительно единичной окружности.
2) Вторая составляющая отображения – 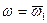 , т.е., как было показано выше,
, т.е., как было показано выше, 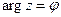 , а
, а 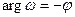 , геометрически означает симметрию относительно действительной оси.
, геометрически означает симметрию относительно действительной оси.
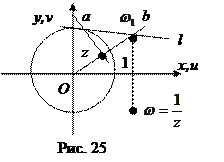 Построение образа точки.
Построение образа точки.
Построим окружность с центром в точке О единичного радиуса (рис. 25). Возьмем внутри окружности точку z. Через точки О и z проведем луч (b) и перпендикулярную ему прямую (а). Через точку пересечения прямой (а) и окружности построим касательную к окружности до пересечения с лучом (b). Это точка 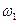 . Построим симметричную ей точку относительно оси (Ох). Эта точка и есть образ точки z при отображении
. Построим симметричную ей точку относительно оси (Ох). Эта точка и есть образ точки z при отображении 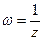 .
.
Вывод: при отображении, реализуемом функцией 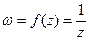 , происходит инверсия: внутренность единичного круга отображается в его внешность и наоборот, при одновременном симметрическом отображении относительно оси (Ох).
, происходит инверсия: внутренность единичного круга отображается в его внешность и наоборот, при одновременном симметрическом отображении относительно оси (Ох).
Замечание 1. При отображении 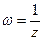 окружности и прямые, не проходящие через точку z = 0, отображаются в окружности, а окружности и прямые, проходящие через эту точку, – в прямые. Прямая считается окружностью бесконечного радиуса.
окружности и прямые, не проходящие через точку z = 0, отображаются в окружности, а окружности и прямые, проходящие через эту точку, – в прямые. Прямая считается окружностью бесконечного радиуса.
Замечание 2.Обратной к простейшей дробно-линейной функции будет функция 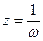 , причем сопряженная функция имеет вид
, причем сопряженная функция имеет вид 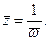
Замечание 3.Если бы аргумент не менялся, т.е. 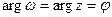 , то при отображении прообраз переходил бы в образ, а образ – в прообраз, т.е. рассматриваемое отображение плоскости в себя само себе обратно. Такие отображения называются инволюциями.
, то при отображении прообраз переходил бы в образ, а образ – в прообраз, т.е. рассматриваемое отображение плоскости в себя само себе обратно. Такие отображения называются инволюциями.
Замечание 4.В некоторых задачах для нахождения образа данной линии при отображении 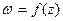 удобно пользоваться следующим правилом: 1) выразить z из
удобно пользоваться следующим правилом: 1) выразить z из 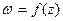 , т.е
, т.е 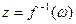 , 2) найти
, 2) найти 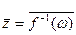 , 3) подставить
, 3) подставить 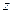 и
и 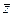 в уравнение линии.
в уравнение линии.
Пример 30. Найти точку, симметричную точке z = 1 + i,относительно окружности 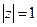 .
.
Дата добавления: 2015-07-14; просмотров: 1898;
