Тригонометрические и гиперболические функции

1) .

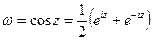Функция однолистна в полуполосе 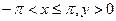и отображает эту полуполосу на плоскость 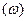с разрезом 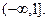Склеивание листов римановой поверхности происходит отдельно по лучу 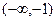и по отрезку [–1,1].

2) .

Функция сводится к 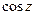при помощи соотношения: .

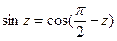3) , .

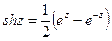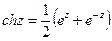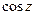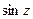Функции сводятся к и при помощи соотношений: ; .

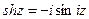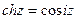7. Функция Жуковского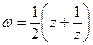

Функция аналитическая во всей плоскости Гаусса за исключением точек z₁ =1, z₂ = –1, z₃ =0, так как .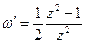

Функция конформна в расширенной плоскости, за исключением точек z₁ =1, z₂ = –1, z₃ =0 и осуществляет конформное отображение как внешности, так и внутренности единичного круга плоскости (z) на плоскость 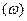с разрезом по отрезку 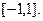Полная плоскость (z) отображается на двулистную риманову поверхность, склеенную крест-накрест по разрезам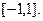

Обратная функция 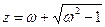– двузначна, причем каждая ветвь осуществляет отображение плоскости 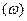с разрезом по 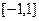на внутренность или внешность единичного круга в плоскости (z).

Конформное отображение, осуществляемое функцией, было использовано Н.Е.Жуковским для решения задач обтекания крыла самолета.