Решение. По первому условию КРЭДа , следовательно, Отсюда x можно найти частным интегрированием: (*)

Найдем .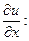

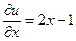По первому условию КРЭДа 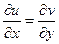, следовательно, 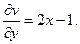Отсюда x можно найти частным интегрированием: (*)

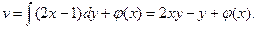По второму условию КРЭДа 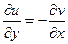, т.е. (**)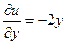

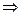
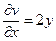С другой стороны, продифференцировав по x (*), получим, что

. (***)

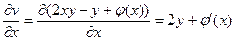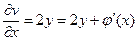
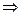
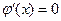
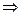
Из (**) и (***) следует: 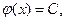С – const.

Подставим в (*): 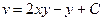. Следовательно,

,

,

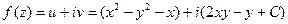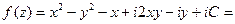
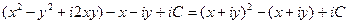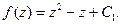
Определение 30.Функция u = u(x,y) называется гармонической, если ее лапласиан равен нулю: .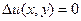

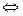
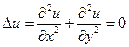Замечание. 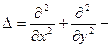оператор Лапласа, 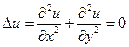– уравнение Лапласа.

Определение 31.Гармонические в области D функции u(x,y) и v(x,y) называются сопряженными гармоническими в области 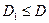, если для их частных производных в области 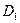выполняются условия КРЭДа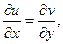

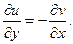
Определение 32.Двесопряженные гармонические функции u(x,y) и v(x,y) называются гармонической парой.

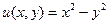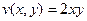Пример 24. Являются ли функции и гармонической парой?