Некоторые свойства аналитических функций.

1. Функция, аналитическая в точке, имеет в этой точке производные любого порядка, которые являются непрерывными в этой точке.

Аналитическая в области D функция дифференцируема, а, следовательно, и непрерывна в этой области.

2. Сумма, разность, произведение и частное (если делитель не равен нулю) двух аналитических в области D функций – аналитическая функция в D.

3. Если 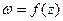– аналитическая функция в замкнутой области D, ограниченной контуром L, то ее значения внутри области D однозначно определяются ее значениями на контуре L.

Если две аналитические в области D функции имеют на контуре L одни и те же значения, то они тождественны во всей области D.

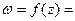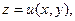
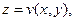
4. (Теорема Дзядыка В.К.) Если u(x,y) +i v(x,y) – аналитическая в области D функция, то площади поверхностей 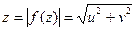, расположенных в трехмерном пространстве (Oxyz) над любой частью области D, равны.

5. Максимум модуля аналитической в области D функции не может располагаться во внутренней точке области D.

6. Пусть 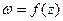– аналитическая в области D функция с областью значений G = 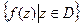и пусть обратная к ней функция 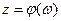аналитична в области G. Тогда сложная функция – аналитична в области G.

Замечаниe.Из свойств аналитических функций легко вывести правила дифференцирования, приведенные выше.

Пример 21.Доказать, что функция 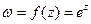аналитическая и найти ее производную.