Решение. .
Продифференцируем: 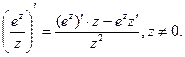
В примере 4 вывели, что 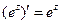 . Найдем производную z, предварительно проверив условия КРЭДа.
. Найдем производную z, предварительно проверив условия КРЭДа. 
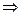 u(x,y) =
u(x,y) = 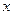 , v(x,y) = y.
, v(x,y) = y.
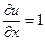 ,
, 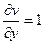
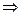
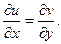
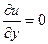 ,
, 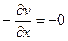
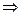
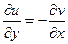 .
.
Условия КРЭДа выполняются по всей плоскости Гаусса, т.е. функция аналитическая, следовательно, существует производная, которую найдем по первой формуле (11):
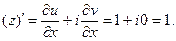
Тогда, 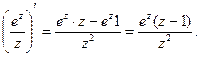
Пример 23.Дана действительная часть u(x,y) = 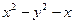 дифференцируемой функции
дифференцируемой функции 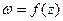 , где
, где 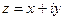 . Найти
. Найти 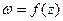 .
.
Дата добавления: 2015-07-14; просмотров: 610;
