Решение. (запишем комплексное число z в показательной форме: и рассмотрим данный предел при , так как если
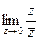
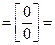 (запишем комплексное число z в показательной форме:
(запишем комплексное число z в показательной форме: 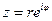 и рассмотрим данный предел при
и рассмотрим данный предел при 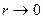 , так как если
, так как если 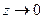 , тогда
, тогда 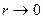 ) =
) = 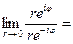
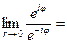
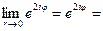 =(по формуле Эйлера)
=(по формуле Эйлера) 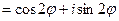 .
.
При различных значениях 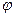 получим различные значения предела, следовательно, он не существует.
получим различные значения предела, следовательно, он не существует.
Пример 9. Доказать непрерывность на всей комплексной плоскости функции 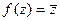 .
.
Дата добавления: 2015-07-14; просмотров: 922;
