Логарифмические функции.
Определение 23.Логарифмом числа 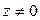 называется такое число A, что справедливо равенство:
называется такое число A, что справедливо равенство: 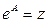 .
.
Логарифмическую функцию комплексного переменного обозначают 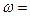 Ln z.
Ln z.
Будем искать вид Ln z в алгебраической форме:
Ln z 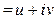 ,
, 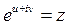 ,
, 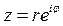 ,
, 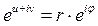 ,
, 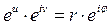 , следовательно,
, следовательно,
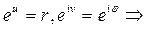
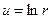 ,
, 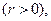
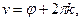
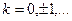 , где
, где 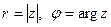 . Тогда
. Тогда
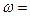 Ln z
Ln z 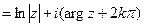 ,
, 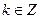 . (8)
. (8)
Функция Ln z – многозначная: в каждой точке, не равной нулю и ∞, она принимает бесконечно много значений. Для каждого k получим определенное значение - логарифм числа z.
При k = 0 получим 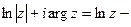 главное значение логарифмической функции, где
главное значение логарифмической функции, где 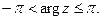 Следовательно, можно записать Ln z
Следовательно, можно записать Ln z 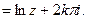
Заметим, что если z – действительное положительное число, то 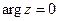 и
и 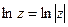 , т.е. главное значение логарифма действительного положительного числа совпадает с обычным натуральным логарифмом этого числа, например, z = 5,
, т.е. главное значение логарифма действительного положительного числа совпадает с обычным натуральным логарифмом этого числа, например, z = 5, 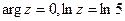 .
.
Свойства 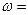 Ln
Ln 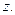
1) Ln 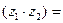 Ln
Ln 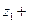 Ln
Ln 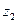 , 2) Ln
, 2) Ln 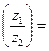 Ln
Ln 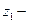 Ln
Ln 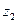 ,
,
3) Ln 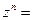 nLn
nLn 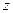 , 4) Ln
, 4) Ln 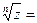
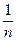 Ln
Ln 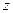 .
.
Доказательство первого свойства.
Ln 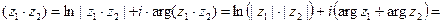
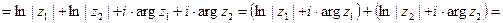 Ln z1 +Ln z2, что и требовалось доказать.
Ln z1 +Ln z2, что и требовалось доказать.
Пример 14.Найти Ln z и главные значения 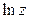 для чисел: а) z =
для чисел: а) z = 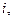 б) z = 1.
б) z = 1.
Решение:
Для решения воспользуемся формулой (8).
а) 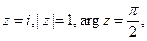
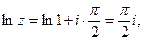
Ln i 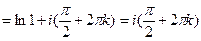 ,
, 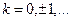
б) 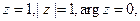
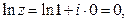
Ln 1 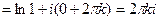 ,
, 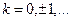
6. Общая степенная функция 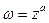 .
.
а) Если а = n – натуральное число, то степенная функция 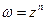 определяется как:
определяется как:
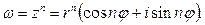
Функция 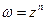 – однозначная.
– однозначная.
б) если 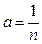 , где
, где 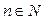 ,то
,то
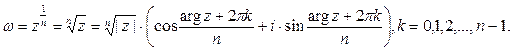
Функция 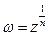 – многозначная, она имеет n значений. Например, при k = 0, получим однозначную функцию.
– многозначная, она имеет n значений. Например, при k = 0, получим однозначную функцию.
в) Если 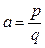 , где
, где 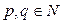 , то
, то 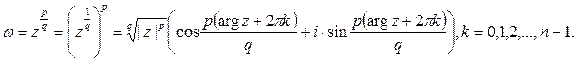
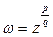 – многозначная функция.
– многозначная функция.
г) Степенная функция 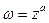 , где
, где 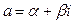 – произвольное комплексное число. Тогда степенная функция
– произвольное комплексное число. Тогда степенная функция 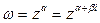 определяется как
определяется как 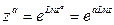 .
.
Функция 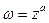 определена для всех
определена для всех 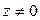 и является многозначной функцией.
и является многозначной функцией.
Главное значение – 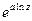 . Если
. Если 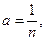
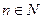 , тогда получим многозначную функцию – корень n-ой степени из комплексного числа:
, тогда получим многозначную функцию – корень n-ой степени из комплексного числа: 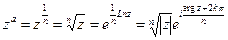 .
.
7. Общая показательная функция 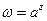 .
.
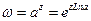 ,
, 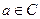
Функция – многозначная. Главное значение – 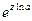 .
.
При 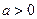 будем полагать, что
будем полагать, что 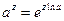 .
.
Пример 15. Найти 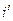 .
.
Дата добавления: 2015-07-14; просмотров: 1269;
