Тригонометрические функции.
При помощи формулы Эйлера можно определить функции 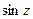 и
и  следующим образом:
следующим образом:
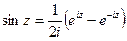 ; (4)
; (4) 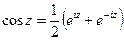 ; (5)
; (5)
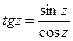 ;
; 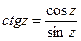 .
.
Если z – действительное число, т.е. z = x (y = 0), то справедливо, что
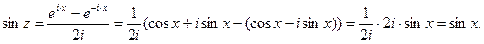
Тригонометрические функции комплексного переменного сохраняют многие свойства тригонометрических функций действительного переменного:
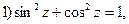
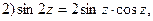
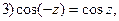
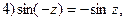
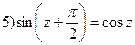 и др.
и др.
Доказательство первого свойства.
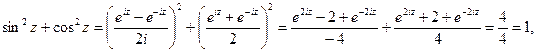 что и требовалось доказать.
что и требовалось доказать.
Замечание.Тригонометрические функции sinz, cosz в комплексной плоскости неограниченны: 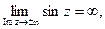
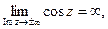 например,
например, 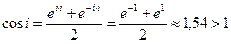
Пример 11. Вычислить: 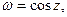 если
если 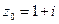 .
.
Дата добавления: 2015-07-14; просмотров: 661;
