Основные элементарные функции комплексного переменного
Отображения, осуществляемые данными функциями, и свойства отображений будут перечислены позднее.
1. Дробно-рациональнаяω = f(z) = 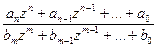
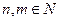 .
.
Частные случаи:
1) Линейная ω = f(z) = az + b, 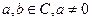 .
.
2) Степенная ω = f(z) = zn, 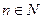 .
.
3) Дробно-линейная ω = f(z) = 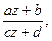
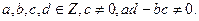
4) Функция Жуковского ω = f(z) = 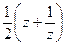 .
.
2. Показательная функцияω = f(z) = 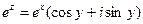 .
.
Некоторые свойства ω = 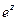 .
.
1) 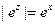 ,
, 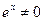 ,
, 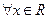 , т.е.
, т.е. 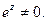
2) 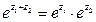 ,
, 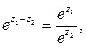
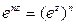 ,
, 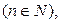
т.е. показательная функция комплексного переменного 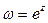 обладает рядом свойств, справедливых для функции действительной переменной.
обладает рядом свойств, справедливых для функции действительной переменной.
3) Показательная функция комплексного переменного является периодической с мнимым основным периодом 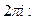
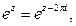
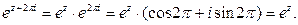
4) ω = 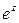 не всегда положительная функция, например:
не всегда положительная функция, например: 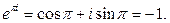
Замечание. В §1 была определена формула Эйлера. Для мнимых показателей она имеет вид: 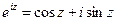 . (3)
. (3)
С помощью формулы Эйлера выводятся формулы для элементарных функций. Например, выражение для показательной функции: 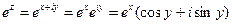 .
.
Также формула (3) применяется для вычисления значений элементарных функций в заданных точках.
Пример 10.Найти 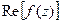 ,
, 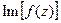 функции
функции 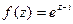 .
.
Дата добавления: 2015-07-14; просмотров: 1464;
