Предел и непрерывность ФКП

Пусть однозначная функция 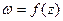 задана в некоторой окрестности точки z0, за исключением, быть может, самой точки z0.
задана в некоторой окрестности точки z0, за исключением, быть может, самой точки z0.
Определение 18.δ – окрестностью точки z0 называется внутренность круга радиуса δ с центром в точке z0 (рис. 14).
Определение 19.Число 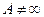 называется пределом функции
называется пределом функции 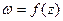 при
при 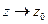 и обозначается
и обозначается 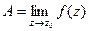 , если для любого положительного ε найдется число δ = δ(ε) > 0 такое, что для всех
, если для любого положительного ε найдется число δ = δ(ε) > 0 такое, что для всех 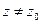 , удовлетворяющих неравенству
, удовлетворяющих неравенству 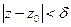 выполняется неравенство
выполняется неравенство 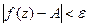 .
.
Определение 20. 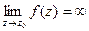 , если для любого R > 0 найдется δ(R) > 0 такое, что для всех
, если для любого R > 0 найдется δ(R) > 0 такое, что для всех 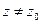 таких что
таких что 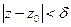 , выполняется неравенство
, выполняется неравенство 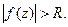
Замечание. Существование предела для функции 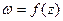 по некоторому фиксированному пути
по некоторому фиксированному пути 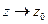 еще не гарантирует существование предела
еще не гарантирует существование предела 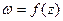 при
при 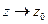 .
.
Определение 21(первое определение непрерывности функции в точке). Функция 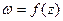 называется непрерывной в точке
называется непрерывной в точке 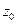 , принадлежащей ее области определения, если
, принадлежащей ее области определения, если 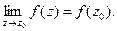
Отсюда можно записать, что для непрерывности функции в точке должно выполняться равенство нулю разности: 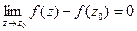 .
.
С учетом того, что предел константы равен самой константе, данное равенство можно записать в виде: 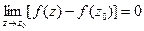 (*).
(*).
Пусть 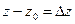 , отсюда
, отсюда 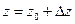 . По условию
. По условию 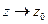 , следовательно,
, следовательно, 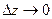 . Рассмотрим приращение функции
. Рассмотрим приращение функции 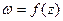 в точке
в точке 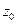 :
:
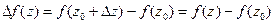 . Подставив полученное равенство в (*), получим второе определение непрерывности функции
. Подставив полученное равенство в (*), получим второе определение непрерывности функции 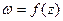 в точке
в точке 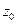 :
:
Определение 21  (второе определение непрерывности функции в точке). Функция
(второе определение непрерывности функции в точке). Функция 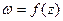 называется непрерывной в точке
называется непрерывной в точке 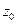 , принадлежащей ее области определения, если
, принадлежащей ее области определения, если 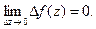
Определение 22. Функция 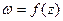 называется непрерывной на некотором множестве, если она непрерывна в каждой точке этого множества.
называется непрерывной на некотором множестве, если она непрерывна в каждой точке этого множества.
Теорема 1 (необходимое и достаточное условие непрерывности).
Для непрерывности ФКП необходима и достаточна непрерывность составляющих ее функций:
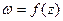 – непрерывна
– непрерывна  u = u(x, y); v = v(x, y) – непрерывны.
u = u(x, y); v = v(x, y) – непрерывны.
Замечание. Равенство 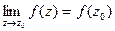 эквивалентно двум равенствам:
эквивалентно двум равенствам: 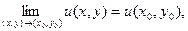
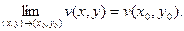
Следствие.Из теоремы следует непрерывность суммы, разности, произведения и частного (знаменатель не равен нулю) двух непрерывных функций.
Замечание. В теории функций комплексного переменного принято считать, что кроме обычных конечных точек комплексной плоскости (z) имеется еще одна несобственная, иначе, бесконечно удаленная точка 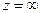 , служащая пределом любой последовательности конечных точек z1, z2,..., для которой
, служащая пределом любой последовательности конечных точек z1, z2,..., для которой 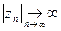 . Комплексная плоскость с добавленной к ней бесконечно удаленной точкой называется расширенной комплексной плоскостью.
. Комплексная плоскость с добавленной к ней бесконечно удаленной точкой называется расширенной комплексной плоскостью.
Пример 7. Вычислить предел 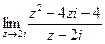 .
.
Дата добавления: 2015-07-14; просмотров: 2817;
