Дифференцируемость ФКП. Аналитические функции
Пусть однозначная функция 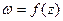 определена в некоторой окрестности точки z, включая саму точку. Придадим аргументу z приращение
определена в некоторой окрестности точки z, включая саму точку. Придадим аргументу z приращение 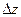 , причем
, причем 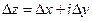 , тогда функция получит приращение
, тогда функция получит приращение 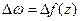 такое, что
такое, что
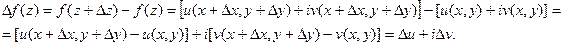
Определение 24.Если существует конечный предел 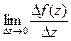 при
при 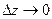 , то он называется производной функции
, то он называется производной функции 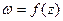 в точке z и обозначается
в точке z и обозначается 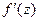 или
или 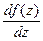 .
.
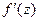 =
= 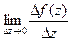
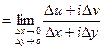 .
.
Определение 25.Функция 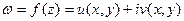 называется дифференцируемой в точке z, если ее приращение можно записать в виде:
называется дифференцируемой в точке z, если ее приращение можно записать в виде:
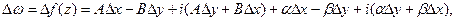 (9)
(9)
где А и В не зависят от 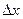 и
и 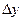 , а
, а 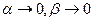 при
при 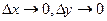 .
.
Теорема 2.Для того чтобы функция 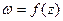 была дифференцируемой в точке z необходимо и достаточно, чтобы она имела в этой точке конечную производную
была дифференцируемой в точке z необходимо и достаточно, чтобы она имела в этой точке конечную производную 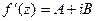 .
.
Доказательствонеобходимости.
Пусть функция 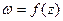 дифференцируема в точке z, тогда ее приращение по определению 25 можно записать в виде (9). Найдем производную функции, пользуясь определением 24:
дифференцируема в точке z, тогда ее приращение по определению 25 можно записать в виде (9). Найдем производную функции, пользуясь определением 24:
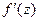 =
= 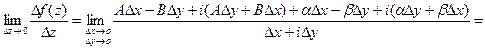
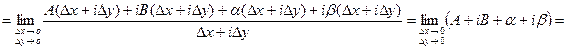
= (по определению 25 величины А и В не зависят от 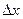 и
и 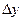 , а
, а 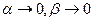 при
при 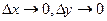 ) = A + iB, что и требовалось доказать.
) = A + iB, что и требовалось доказать.
Определение 26. Если 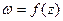 имеет производную в точке z, то она называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке некоторой области D плоскости Гаусса, называется дифференцируемой в области D.
имеет производную в точке z, то она называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке некоторой области D плоскости Гаусса, называется дифференцируемой в области D.
Теорема 3.Дифференцируемая функция 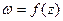 в точке z (или в области D) непрерывна в этой точке (или области).
в точке z (или в области D) непрерывна в этой точке (или области).
Дата добавления: 2015-07-14; просмотров: 822;
